|
The concept of consecutive integers is popular when writing
algebraic expressions and equations.
 |
Consecutive integers are numbers that continuously follow each other, in a counting order or pattern. The difference between two adjacent numbers is always the same value. The order is generally from smallest to largest. |
|
The counting numbers, for example, are consecutive integers.
Notice that the difference between two adjacent numbers is always "one".
Yes, the missing number is "6".
If we represent one of these consecutive integers by the letter "n", then
•
the next consecutive integer will be represented by "n + 1"
• the next consecutive integer beyond this will be "n + 2" and so on.
Remember, the number "1" is added to each number to get the next number.
n, n + 1, n + 2, n + 3, n + 4, n + 5, . . .
Negative integers can also be consecutive integers.
. . . , -6, -5, -4, -3, -2, -1, 0, 1, . .
.
The even counting numbers, for example, are consecutive even integers.
Notice that, this time, the difference between two adjacent numbers is always "two".
Yes, the missing number is "10".
If we represent one of these even consecutive integers by the letter "n", then
•
the next consecutive even integer will be represented by "n + 2"
• the next even consecutive integer beyond this will be "n + 4" and so on.
Remember, the number "2" is added to each number to get the next number.
n, n + 2, n + 4, n + 6, n + 8, n + 10, . . .
Negative even integers can also be consecutive even integers.
. . . , -10, -8, -6, -4, -2, 0, . . .
Letting x = -10, we can write:
. . . , x - 2, x, x + 2, x + 4, x + 6, x + 8, x + 10, . . .
where x + 10 = 0.
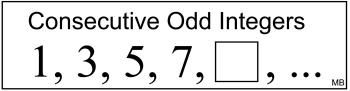
The odd counting numbers, for example, are consecutive odd integers.
Notice that, again, the difference between two adjacent numbers is always "two".
Yes, the missing number is "9".
If we represent one of these consecutive odd integers by the letter "n", then
•
the next odd consecutive integer will be represented by "n + 2"
• the next consecutive odd integer beyond this will be "n + 4" and so on.
Remember, the number "2" is added to each number to get the next number.
n, n + 2, n + 4, n + 6, n + 8, n + 10, . . .
Negative odd integers can also be consecutive odd integers.
 While the consecutive even integers and consecutive odd integers are represented in the same manner, n, n + 2, n + 4, ..., remember that they are always different in their "starting values" for n.
For consecutive even integers, n is always an even number, while for consecutive odd integers, n is always an odd number. For this course, whether n is odd or even is indicated in the statement of the problem.
FYI: So, what would happen if we were not able to determine
if our "starting value" is even or odd?
Let's think for a minute about the concept of "even" and "odd".
We saw in the lesson on Even and Odd Integer Expressions that
an even integer is often represented by 2n.
(so no matter the value of n, 2n will always be even.)
and that an odd integer is often represented by 2n + 1.
(so no matter the value of n, 2n + 1 will always be odd).
So, if a problem stated:
"If n is an integer, represent three consecutive even integers."
If is unclear if n is odd or even to start.
Best answer: 2n, 2n + 2, 2n + 4 which guarantees even values.
"If n is an integer, represent three consecutive odd integers."
Again, unclear if n is odd or even to start.
Best answer: 2n + 1, 2n + 3, 2n + 5 which guarantees odd values.
1. a. Determine the next three consecutive integers: 19, 20, ___, ___, ___
b. Determine the next three consecutive even integers: -6, -4, -2, ___, ___, ___
c. Determine the next three consecutive odd integers: 47, 49, ___, ___, ___
d. Starting with even integer b, determine the next three consecutive even integers:
b, ___, ___, ___
Solution:
a) 21, 22, 23
b) 0, 2, 4
c) 51, 53, 55
d) b +2, b + 4, b + 6
2. The first of 6 consecutive integers is represented by n. What value needs to be added to this first term to express the sixth term?
Solution: Represent the six consecutive integers as n, n + 1, n +
2, n + 3, n + 4, n + 5.
Notice that the pattern to determine the value added for each term, is to add one less than the position of the term in the listing. The sixth term is 5 more than the first term.
ANS: The value of 5.
3. Which expression is equivalent to the sum of three consecutive even integers, starting with even integer x?
[1] 3(x + 1) [2] x3+ 6 [3] 3(x + 2) [4] x2 + 6
Solution: Represent the three consecutive even integers as x, x + 2, and x + 4 with the sum being 3x + 6.
3x + 6 = 3(x + 2)
ANS: Choice [3] .3(x + 2)
4. If the third term in a listing of positive consecutive odd integers is expressed
as x + 12, which expression represents the first term in this listing?
[1] x + 6 [2] x + 7 [3] x + 8 [4] x + 9
Solution: Consecutive odd integers are represented as being two units apart.
Working backward from x + 12, we have x + 12, x + 10, x + 8 as the three consecutive odd integers, with the first term being x + 8.
ANS: Choice [3] x + 8.
See: "Working with Consecutive Integer Equations"
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
