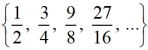There are several special types of sequences that can be classified as explicit sequences.
That is, sequences for which a formula can be used to determine any term.
The geometric sequence is another one of these special types of explicit sequences.

Geometric Sequences
mult
Multiply




The geometric sequence is based upon the multiplication of a constant value
to arrive at the next term in the sequence.

Consider the sequence: { 3, 6, 12, 24, 48, ... }

Geometric sequences follow a pattern of multiplying a fixed amount (not zero) from one term to the next. The number being multiplied each time is called the common ratio, r.
To find the common ratio, divide the second term by the first term.
The common ratio may be either positive or negative.

For this sequence, the common ratio is 2.


Term Number
Term
Subscript Notation
1
3
a1
2
6
a2
3
12
a3
4
24
a4
5
48
a5
6
96
a6
n
dotdotdot
an
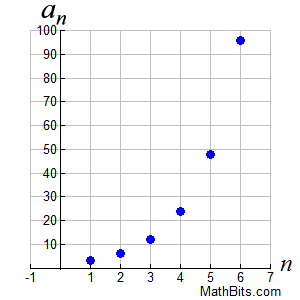
geographfunctionex
This sequence is graphed in the first quadrant.
Sequences are graphed as a series of dots.
Remember that the domain consists of the natural numbers, {1, 2, 3, ...}, and the range consists of the terms of the sequence.

Notice that this sequence has an exponential appearance. It may be the case with geometric sequences that the graph will increase (or decrease). The rate of change will increase (or decrease) as the value of n increases (it is not constant).

This graph grows (or decays) by a constant percent rate per unit interval relative to another making it a discrete "exponential" function.
(Remember, the graph of a discrete function is a series of dots.)

divider dash

bullet Repeatedly multiplying "r ":

If we think about multiplying "r " times the first term, we get the second term: a2 = a1• r.

Multiplying "r " times that second term, we get the third term: a3 = a1• r • r = a1• r2 .

By continuing this process, we can generate a symbolic geometric sequence:

a1 ,  (a1• r ) ,  (a1 • r 2 ) ,  (a1 • r 3 ) , ... , (a1 • r (n - 1) )
  term 1   term 2 term 3 term 4   term n

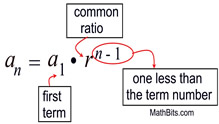
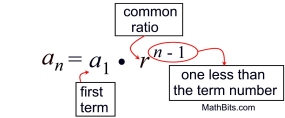
From this pattern, we can see a formula emerge for the nth term:    an = a1 • r (n - 1).

Note how (n - 1) popped out in relation to r.
The (n - 1) is needed since r was not multiplied to obtain the first term.
The r started working with the second term.

We just generated a format for creating explicit formulas for geometric sequences.

 an = a1 • r (n - 1)    YEA!!!!



Geometric Sequence:     an = a1 • r (n - 1)  


divider dash


Finding an Explicit Formula for this Sequence
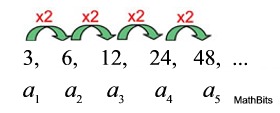
{ 3, 6, 12, 24, 48, 96, ... }

 



We know this is a geometric sequence (the same number, 2, is multiplied times each term to get to the next term).

We have seen that trying to "find" an explicit formula for a sequence
might be difficult, or even impossible.

But, if your sequence is geometric, you will be able to find the explicit formula easily.
Simply use the first term, a1, and the common ratio, r,
in the format  an = a1• r (n - 1)  that we discovered in the section above.  

 

funcformulaG

Explicit formula:  an = 3 • 2n - 1

If you compare the term number with the powers of the common ratio, 2, you will see a pattern for an explicit formula:

         

To get the explicit formula, plug in the first term, 3, and the common ratio, 2.
an = 3 • 2n - 1

Now that you have the explicit formula, find the 20th term of this sequence.

Replace n with 20 in the explicit formula:  an = 3 • 2n - 1
a20 = 3 • 2 20 - 1 = 3 • 524288 = 1572864 = 1,572,864 ANSWER


divider dash


bullet Summary of Finding an Explicit Formula for a Geometric Sequence.

Process of writing an explicit formula for a geometric sequence:
1. Determine if the sequence is geometric
(Did you multiply, or divide, the same amount from one term to the next?)
2. Find the common ratio. (The number you multiply or divide.)
3. Create an explicit formula using the pattern a1 • r n - 1
geoformulaexplicit
an = the nth term in the sequence
a1 = the first term in the sequence
n = the term number
r = the common ratio
funcgeoformulaB
{3, 6, 12, 24, 48, 96, ...}
first term = 3, common ratio = 2
explicit formula: an= 3 • 2n-1

divider dash

bullet Working with Geometric Sequences:

Find the common ratio.

Geometric Sequence: Common Ratio, r:
{ 1, 4, 16, 64, 256, ... }
r= 4. A 4 is multiplied by each term to arrive at the next term.
{ -2, 4, -8, 16, -32, ... }
r = -2. A -2 is multiplied by each term to arrive at the next term.
r = 3/2. A 3/2 is multiplied by each term to arrive at the next term.

divider dash

Find a specific term.

Geometric Sequence Formula: Requested Term:
Find the 4th term of an geometric sequence if the first term is 6 and the common ratio is 2.
The sequence looks like: 6, __, __, x
Multiply by 2 between terms, we get: 6, 12, 24, 48
The fourth term is 48.
Find the 5th term of the sequence
an= 2(-3)n - 1
n = 5
a5= 2(-3)5 - 1 = 162
Find the first three terms of the geometric sequence
an= 18 (2)n - 1
What is the common ratio?
a1 = 18(2)0 = 18.
a2 = 18(2)1 = 36.
a3 = 18(2)2 = 72
The common ratio is 2.


divider dash

Using an explicit formula.

Geometric Sequence Formula: Explicit formula:
The first term of the sequence is 4 and the common ratio is -3.
Find the fifth term.
r = -3
Use: an = a1 • r (n - 1)
 a5= 4 • (-3)5 - 1 = 324
a1 = 2 and a2 = 6
Find an explicit formula for this sequence.
The common ratio 3.
Use: an = a1 • r (n - 1)
an = 2 (3)n - 1
What is the formula for the nth term of the sequence { 54, 18, 6 , 2, ...}?
r = 1/3.
Use: an = a1 • r (n - 1)
an = 54 (1/3)n - 1          

For application word problems for sequences,

see BEWARE: Sequences and Word Problems

and Examples of Working with Sequences.

divider dash


ti84c
For calculator
help with
sequences
click here.

Arrow down to
"In Func MODE"

divider


NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".