We have worked with arithmetic and geometric sequences in numerical situations,
and we know the explicit an formulas associated with each.
But, working with these sequences in real world situations can be a bit tricky.

Working with "entities that are changing during a time period" can be tricky,
such as working with "growth" or "decay".
In relation to a time period, do you want to know the growth number
at the START of a specific time period, or at the END of that time period?
 Carl planted a 4 inch sunflower plant. The plant grows 3 inches each week. How tall is the plant at the end of 5 weeks?
Carl planted a 4 inch sunflower plant. The plant grows 3 inches each week. How tall is the plant at the end of 5 weeks?
In the diagram below, we see the plant growing 3 inches each week.
The sequence starts with the value 4 inches,
and 3 inches is added to form each term of an arithmetic sequence.
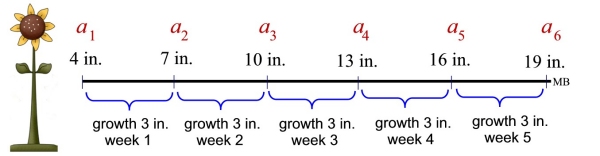
NOTE: At the end of week 5, we are at term a6.
| Height |
an |
4 |
7 |
10 |
13 |
16 |
19 |
| Week |
n |
1 |
2 |
3 |
4 |
5 |
6 |
When we apply the arithmetic fomula using a1 = 4 and d = 3, we have:
an = 4 + (n - 1) 3
Substituting the time of 5 weeks, we get:
a5 = 4 + (5 - 1) 3 = 16 inches
 |
This answer is WRONG!
It may appear that we followed the formula as we have done in the past, but this time the result is not true. We needed to look more carefully at that diagram above. Using n = 5 gives us the height of the plant at the beginning of the 5th week, not the ending of the 5th week.
The ending of the 5th week = the beginning of the 6th week.
|
|
So, what do we do to fix this problem?
You have 2 choices.
You can change the starting value to 7 and use the regular formula. Think of it as 7 being the first acutal growth number, since 4 was not a
number signifying growth that occurred after planting.
(Or, you can add 1 to n since we need to be at the end,)
an = 7 + (n - 1) 3
a5 = 7 + (5 - 1) 3 = 19 in.
|
You can adjust the formula to deal with these types of situations, Change (n- 1) to simply (n).
You may see textbooks using this option and substituting "t" (time) for "n".
an = a1 + (n) d
at = a1 + (t) d
a5 = 4 + 5(3) = 19 in.
|
Correct answer: 19 inches.

 A specific strain of bacteria doubles every 5 hours. The researchers currently have 300 bacteria.
A specific strain of bacteria doubles every 5 hours. The researchers currently have 300 bacteria.
a) Establish a formula to represent the growth of the bacteria.
b) How many bacteria will be present at the end of the 15th hour?
In the diagram below, we see the doubling of the bacteria over 15 hours.
The sequence starts with the value 300 bacteria,
and doubling of the bacteria every 5 hours to form each term of a geometric sequence.
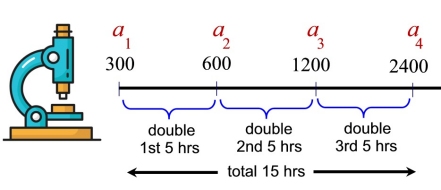
NOTE: At the end of 15 hours, we are at term a4.
| Bacteria |
an |
300 |
600 |
1200 |
2400 |
| Time periods of 5 hrs each. |
n |
1 |
2 |
3 |
4 |
When we apply the geometric fomula using a1 = 300 and r = 2, we have:
an = a • rn - 1
Substituting 3 for the three 5 hour periods in 15 hours, we get:
a5 = 300 • 23 - 1 = 1200 bacteria
 |
Again, this answer is WRONG!
The diagram of the bacteria growth shows that the third 5 hour time interval will end at 2400 bacteria. As seen in the previous example, the answer is at the end of the 3rd interval (not the beginning).
The ending of the 3rd interval = the beginning of the 4th interval. |
|
a) Formula: an = a • rn
b) Correct answer: 2400 bacteria.



