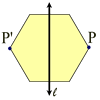
Line symmetry occurs when two halves of a figure are mirror images of each other when reflected across a line.
• The line of symmetry is the line which divides the figure into two mirror images.
• To determine if a figure has line symmetry, fold the figure along the supposed line of symmetry to see if the two halves coincide.
• A figure has a line of symmetry if the figure can be mapped onto itself by a reflection in the line.
|
A set of points has line symmetry if and only if there is a line, l, such that the reflection through l of each point in the set is also a point in the set. |
|
|
Line symmetry can be observed in a variety of situations:
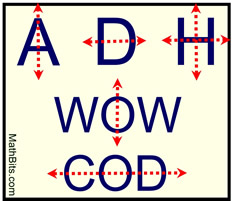
In Printed Letters: |
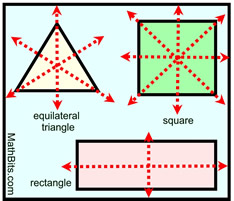
In Geometric Figures: |
In Function Graphs: |
In certain fonts, letters/words possess line symmetry.
 |
Certain geometric figures possess line symmetry.
|
Certain function graphs possess line symmetry.
|
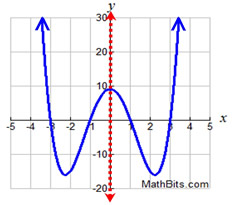
In Photographs:
|
In Art Work:
|
In Math Symbols:
|
A photo of a water reflection creates line symmetry.
|
Artists know that symmetric shapes are the most pleasing to the eye.
 |
Certain math symbols, numbers, and answers.
 |
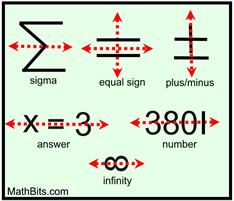If a plane intersects a three dimensional figure such that one half of the figure is the reflected image of the other half, the figure possesses "plane symmetry". The two halves of the figure are mirror images in the plane. Plane symmetry is the three dimensional version of line symmetry.
Plane symmetry can be observed all around us:
Real objects are never "perfectly" symmetrical as there are always tiny flaws (even at the atomic level) that destroy the notion of "perfect" symmetry. We, however, refer to a real object as having symmetry if it does so as a whole, apart from minor defects.
In Butterflies: |
In Flowers: |
In Architecture: |
Biologists call a line of symmetry a "bilateral symmetry".
 |
Botanists refer to this symmetry as "zygomorphic" (bilateral symmetry).
 |
Architects know symmetrical shapes are pleasing.
 |
In Packaging: |
In Food Service: |
In Life: |
Many boxes have plane symmetry, in several directions.
 |
Cones support many delicious confections, along with plane symmetry. 
|
Animal (and human) forms possess bilateral symmetry.
|
How symmetric are you?
The photos below show the "normal face" in the center. The photo on the left duplicates the left side of the face along its line of symmetry. The photo on the right duplicates the right side of the face along its line of symmetry.
Duplicate Left Side |
Normal Face |
Duplicate Right Side |
 |
 |
 |
The photograph of this young woman's face shows a strong amount of vertical (bilateral) symmetry.
Duplicate Left Side |
Normal Face |
Duplicate Right Side |
 |
 |
 |
By not looking directly at the camera, the photograph of this young man's face created a couple of interesting "new" looks.
If you want to see what you would look like if either side of your face was duplicated "exactly", find a photo of yourself looking at the camera. Hold a mirror perpendicular to your facial line of symmetry on the photo. Look at your "new" self in the mirror.
Or, you can use your computer to cut apart your photo.
Paint Shop Pro |
Adobe Photoshop |
MS Photo Draw |
(1) Open your photo and save it under a new name so as not to damage your original photo.
(2) Use your selection tool to outline one side (half) of the photo.
(3) Under IMAGE, choose MIRROR.
(4) Drag the new image so it will create a new face.
(5) CROP your new image, and
(6) SAVE the photo.
(7) Repeat the process for the other side of the face. |
(1) Open your photo and save it under a new name so as not to damage your original photo.
(2) Use the RECTANGULAR MARQUEE TOOL to select one side (half) of the photo.
(3) EDIT / COPY.
(4) EDIT / PASTE.
(5) Use the MOVE TOOL to position the half of the photo over the right half.
(6) Select IMAGE / ROTATE / FLIP LAYER HORIZONTAL to flip the other half.
(7) Use the BLUR TOOL to soften the vertical line in the middle.
(8) SAVE the photo.
(9) Repeat the process for the other side of the face. |
(1) Open your photo and save it under a new name so as not to damage your original photo.
(2) Select CROP SIZE, Cut Out, square shape.
(3) Outline half of the photo passing through center of face. Choose COPY.
(4) PASTE new image twice.
(5) Choose one, pick Arrange, Flip Horizontal.
(6) Move halves together.
(7) Repeat the process for the other side of the face. |
Point symmetry exists when a figure is built around a single point called the center of the figure. For every point in the figure, there is another point found directly opposite it on the other side of the center, at the same distance from the center.
• in a point symmetry, the center point is the midpoint of every segment formed by joining a point to its image.
• a figure has point symmetry if when turned upside-down it looks the same.
• a figure with point symmetry will appear the same after a 180 degree rotation.
• point symmetry is a special form of rotational symmetry of Order 2.
Observing Point symmetry:
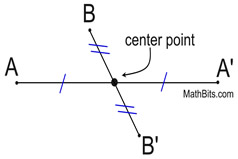Points A and B are reflected through the center point.
The center point becomes the midpoint of the segments from A to A', and from B to B'. |
Some fonts create letters and words with point symmetry.  |
The two of spades has point symmetry. It looks the same right-side up or upside-down.
 |
A geometric figure has rotational symmetry if the figure is the image of itself under a rotation about a point through an angle whose measure is strictly between 0º and 360º. The angles of 0º and 360º are excluded since nothing new happens, and the angle of rotation will be a factor of 360.
•
The number of positions in which the object looks exactly the same is called the order of the symmetry.
•
When determining order, the last rotation returns the object to its original position (360º).
• The angles of 0º and 360º are not listed as they are the starting locations.
•
Order 1 implies no true rotational symmetry exists, since a full 360 degree rotation is needed to again display the object with its original appearance.
• Order 2 implies a duplicate image at a rotation of 180º (splitting 360º into 2 equal parts).
• Order 3 implies a duplicate image at 120º and 240º (splitting 360º into 3 equal parts).
• Order 4 implies a duplicate image at 90º, 180º, and 270º (splitting 360º into 4 equal parts).
And so on ...
Order 2: |
Order 3: |
Order 4: |
|
Triskelion on the Isle of Man flag.
|
|
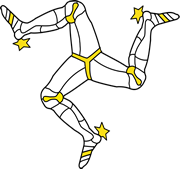
Order 5: |
Order 6:
|
Grid Pattern: (order 4)
|
Botanists refer to this as "radial symmetry".
|
A 780 ft.' crop circle in a double triskelion pattern. 
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
