|
The transformations you have seen in the past
can also be used to move and resize graphs of functions.
| Translation: Vertical Shift: f (x) + k |
 A function can be moved up (or down) by adding a constant to the y-value.
(Remember: the y-value is also the f (x)-value.)
This movement is called a vertical shift.
It is movement along the y-axis.
The constant value to be added is represented as "k"
(x, f (x)) → (x, f (x) + k)
Vertical Shift: f (x) + k
• k > 0 slides straight up
|
| • k < 0 slides straight down |
| • k = 0 no movement |
|
When dealing with "k", the sign (±) indicates
the "direction" of the movement.
The actual distance traveled is always positive, | k |,
as distance and units of measurement are positive. |
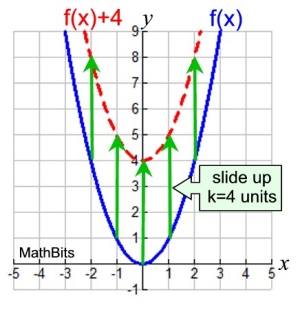
Given: f (x) = x2 and k = 4
A vertical shift, will add four
to the outputs of f (x).
Vertical Shift:
f (x) + 4 = x2 + 4
The new function can be renamed:
g (x) = x2 + 4 |
Every point in a function graph will move up (or down) in a vertical shift.
(x, y) → (x, y + k)
 A vertical shift deals with changing ONLY the y-values.
a) Graph  .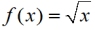
b) State the equation, g(x), that represents a vertical shift of k = -3 to f (x).
c) Graph g(x). Describe how the graph of g(x) is formed.
d) The point (1,1) is located on f (x). What will be the coordinates of this point after the vertical shift?
e) State the domain and range of f (x) and g(x). |
Solutions:
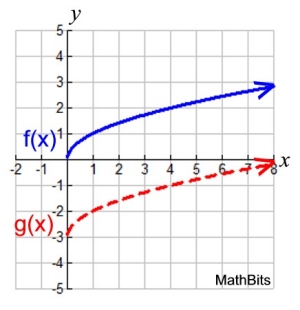
a) See graph
b) g(x) = f (x) - 3
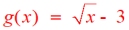
c) See graph.
Every point of f (x) slides straight "down" 3 units,
forming function g(x). The graph of g(x) is the function
f (x) shifted "down" three units.
d) The point will be (1, -2). The y-value changed by 3 units in the negative direction (down).
e) Domain of f (x): [0,∞). Domain of g (x): [0,∞)
Range of f (x): [0,∞). Range of g (x): [-3,∞)
|
 |
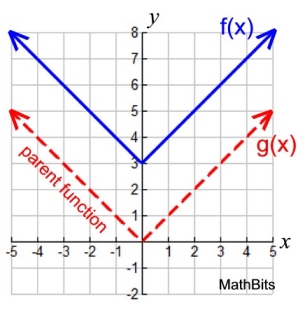
a) Graph f (x) = | x | + 3 using your knowledge of its parent function.
b) Describe the transformation that has occurred in this problem from the parent function.
c) The turning point for the parent function is located at (0,0). What are the coordinates of the turning point of f (x)?
d) State the domain and range of the parent function and of f (x),
|
Solutions:
a) The parent function is the simplest absolute value function which is g(x) = | x |
(You need to remember the graph of the parent function of absolute value.)
b) The parent function, g(x), was transformed by a vertical shift of k = 3 to produce the function f (x).
c) (0,3)
d) Domain of f (x): (-∞,∞). Domain of g (x): (-∞,∞)
Range of f (x): [3,∞). Range of g (x): [0,∞) |
 |
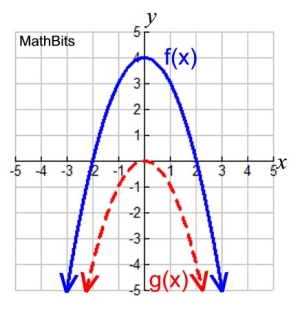
This example combines reflection with vertical shift.
Given the graph at the right showing functions f (x) and
g(x) where f (x) is the vertical shift of g(x).
a) Describe the parent function associated with these graphs.
b) Describe the transformation(s) that occurred in this problem.
c) Write an equation for f (x).
d) State the coordinates of the maximum point of g(x).
State the coordinates of the maximum point of f (x).
e) State the domain and range of f (x) and g(x).
|
 |
Solutions:
a) These graphs are a parabolas, so the parent function is y = x2. BUT, the parent function opens upward, and these "children" are opening downward. So, we will need to adjust the parent function to open downward, by reflecting it over the x-axis, to get g (x) = -x2.
b) The reflected parent function, g(x), was then transformed by a vertical shift of k = 4 to produce the function f (x).
c) f (x) = -x2 + 4
d) (0,0) and (0,4)
e) Domain of f (x): (-∞,∞). Domain of g (x): (-∞,∞)
Range of f (x): (-∞,4]. Range of g (x): (-∞,0]
|
S U M M A R Y
Translation of a Function: f (x) + k called a Vertical Shift |
Translation vertically (upward or downward)
f (x) + k translates f (x) up or down |
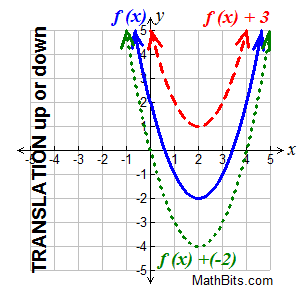 Changes occur "outside" the function
(affecting only the y-values). |
Vertical Shift:
This translation is a "slide" straight up or down.
• if k > 0, the graph translates upward k units.
• if k < 0, the graph translates downward k units.
In the past, on a coordinate grid, you used the formula (x,y) → (x,y + k) to move a figure upward or downward.
Keeping in mind that now y = f (x),
we can replace y with f (x) and get:
(x, f (x)) → (x, f (x) + k).
Remember, you are adding the value
of k to the y-values of the function, where the y-values are now called f (x). |
vertical shift |
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
