Features of Function Graphs MathBitsNotebook.com Topical Outline | Algebra 1 Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

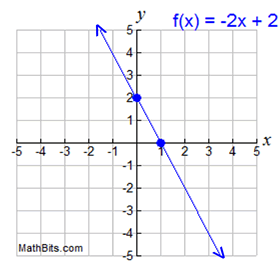
To find the y-intercept, set x = 0, and solve for y. Remember: the y-intercept will have an x-coordinate of 0. y = f (x) = -2x + 2 y = -2(0) + 2;    y = 2     y-intercept: (0,2) (Yes, you can also read the y-intercept, b, from the function equation if it is in y = mx + b form.) To find the x-intercept, set y = 0, and solve for x. Remember: the x-intercept will have a y-coordinate of 0. y = f (x) = -2x + 2 0 = -2x + 2;     2x = 2;     x = 1     x-intercept: (1,0) x-intercepts may also be referred to as "roots" or "zeros" since they are where f (x) = 0.

y-values positive or y-values negative

The positive regions of a function are those intervals where the function is above the x-axis. It is where the y-values are positive (not zero). The negative regions of a function are those intervals where the function is below the x-axis. It is where the y-values are negative (not zero). y-values that are on the x-axis are neither positive nor negative. The x-axis is where y = 0.

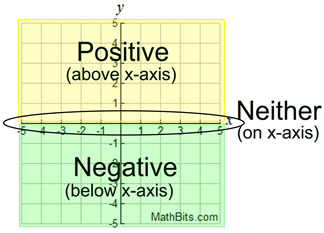
Some functions are positive over their entire domain (All y-values above the x-axis.) 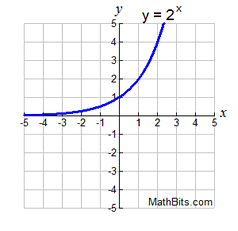positive: -∞ < x < +∞ or "all Reals", or (-∞,+∞)

Some functions are negative over their entire domain. (All y-values below the x-axis.) 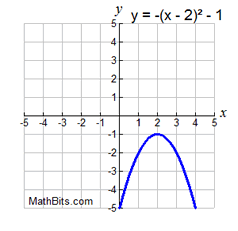negative: -∞ < x < +∞ or "all Reals", or (-∞,+∞)

Some functions have both positive and negative regions. (y-values above and below x-axis) 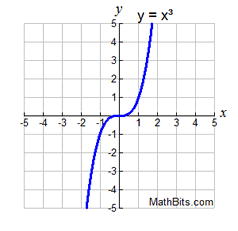positive: x > 0 or (0,+∞) negative: x < 0 or (-∞,0) (do not include zero)

Secret to Finding the Intervals! The secret to correctly stating the intervals where a function is positive or negative is to remember that the intervals ALWAYS pertain to the locations of the x-values. Think of reading the graph from left to right along the x-axis. Do NOT read numbers off the y-axis for the intervals. Stay on the x-axis!

The discussion on this page will refer to "strictly" increasing and "strictly" decreasing.

Increasing: A function is increasing, if as x increases (reading from left to right), y also increases . In plain English, from left to right, the graph goes up-hill. The graph has a positive slope. By definition: A function is strictly increasing on an interval, if when x1 < x2, then   f (x1) < f (x2). If the function notation is bothering you, this definition can also be thought of as stating x1 < x2 implies y1 < y2. As the x's get larger, the y's get larger. 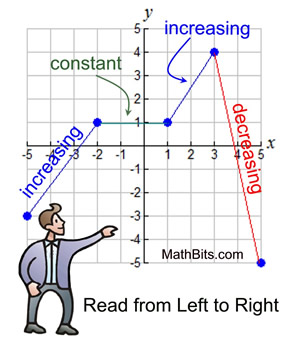Example: The function (graph) at the right is increasing from the point (-5,-3) to the point (-2,1), which is described as increasing when -5 < x < -2 . Using interval notation, it is described as increasing on the interval (-5,-2).

It also increases from the point (1,1) to the point (3,4), described as increasing when 1 < x < 3. Using interval notation, it is described as increasing on the interval (1,3).

Example: The graph shown above is decreasing from the point (3,4) to the point (5,-5), described as decreasing when 3 < x < 5.
Using interval notation, it is described as decreasing on the interval (3,5).

Constant: A function is constant, if as x increases (reading from left to right), y stays the same. In plain English, from left to right, the graph goes flat (horizontal).
The graph has a slope of zero.

Example: The graph shown above is constant from the point (-2,1) to the point (1,1), described as constant when -2 < x < 1. The y-values of all points in this interval are "one".
Using interval notation, it is described as constant on the interval (-2,1).

Intervals of increasing, decreasing or constant ALWAYS pertain to x-values. Do NOT read numbers off the y-axis. Stay on the x-axis for these intervals!

Intervals of Increasing/Decreasing/Constant: Interval notation is a popular notation for stating which sections of a graph are increasing, decreasing or constant. Interval notation utilizes portions of the function's domain (x-intervals). For the graph shown above, we would write:

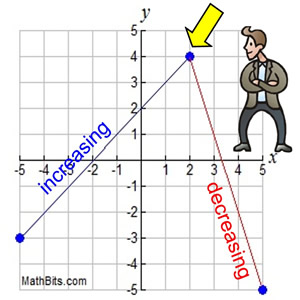
Differing notations for increasing intervals: Regarding intervals of increasing or decreasing on a graph, it is a popular convention to use only "open" interval notation. However, it is also considered correct to use either "open" or "closed" notation when describing intervals of increasing or decreasing. References to ± infinity are always "open" notation. Take a look at the point (2,4) in the graph at the right. Does that point belong to the increasing interval? The decreasing interval? Both intervals? Neither interval? Well, the answer may be both, neither, or a combination, depending upon the convention you are following. You may say "increasing on the interval (-5,2) or the interval [-5,2], or the interval (-5,2], or the interval [-5,2)." Just be consistent with the convention you are using. Functions increase on intervals, not at points. The graph is neither increasing nor decreasing at the point (2,4). However, if a function increases on an "open" interval, then adding the endpoints will not change this fact (as long as the endpoints are in the domain). This site will be using "open" interval notation to represent intervals of increasing and decreasing. Ask your teacher which notation convention is preferred in your classroom.

For maximum/minimum, symmetry, and end-behavior, see More Function Features.
For continuous, roots, and multiplicity of roots, see Factoring and Graphing Polynomials.