|
"We will be examining quadratic trinomials of the form ax2 + bx + c."
We have seen the "Split the Middle" (or "ac") method for factoring trinomials where a ≠1.
Now, we will look at another "short cut" method that seems quite popular,
referred to as the "Slide and Divide" Method or the "Slip and Slide" Method. This method is so named because coefficients undergo a variety of slipping, sliding and dividing maneuvers.
 The "Slide and Divide" Method of Factoring Trinomials:
There are four basic steps that are followed in this method that appear in the table below.
Factor a trinomial of the form ax2 + bx + c, a ≠ 1 : |
Factor: 3x2 + 13x - 10 |
1: "Slide" the leading coefficient, a, over to the constant term, c, at the end of the trinomial, and multiply those two values.
Replace the constant, c, with this new a times c.
Remove the leading coefficient.
Whoa!!! This new trinomial is no longer equivalent to the original trinomial. |
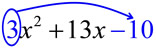x2 + 13x - 30 |
2: Factor the new trinomial expression.
The new trinomial can be factored easily since it has a leading coefficient of 1. |
(x + 15)(x - 2)
|
3: "Divide" both of those numeric factors of -30 by the value "slipped" over in Step 1 (which is 3). Another non-equivalent expression? |
|
4: Simplify the fractions where possible. "Slide"any demonimator left over up next to the variable.
In this case, "slide" the 3 to be the coefficient of x. Slide the denominator?
|
(x + 5)(3x - 2) Answer |
OKAY!!! What about that move of changing the original trinomial?
And, how about "sliding" that denominator around in the parentheses?
 |
"Slide and Divide" Method for Factoring Trinomials
This "short cut" method does not get the "Good Math Keeping" seal of approval. While this method yields correct results, the journey to get there will make no rational mathematical sense to students not versed in what is actually happening mathematically behind the scenes in this method. |
On first glance, this method could be described as a series of errors in mathematical judgement. The original expression's visibility is lost throughout the solution and denominators are moving around at will in sets of parentheses.
Unless students are well versed in the actual mathematical reasoning behind this short cut method, its use could prove to be detrimental. A first glance, this method seems to randomly make magical mathematical changes.
Such changes, if done by students, would be marked as errors. |
|
But, surprisingly, this process is actually mathematically legal when you look at the entire process. It just looks "hokey" when you try to explain this concept as a limited step-by-step process and by-pass what is actually happening.
Let's break this process down to see what is really going on.
Unfortunately, the justification involves variable substitution
which is most likely beyond the mathematical skills of younger mathematicians.
| Rationale for factoring 3x2 + 13x - 10 by "Slide and Divide" Method. |
While this method is mathematically legitimate, the "short cut" steps will be extremely hard to remember, as there is no mathematical support behind the magical changes in the four steps.
But, it does work!
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
