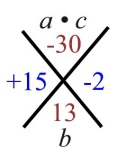"We will be examining quadratic trinomials of the form ax2 + bx + c."
Factoring trinomials with a leading coefficient not equal to 1,
and with no common factors, can be difficult and time consuming.
The process shown on this page may make that factoring a bit easier.
Notice, when we multiply (x + 4)(x + 6) we get x2 + 4x + 6x + 24 which equals x2 + 10x + 24.
Whenever you multiply two binomials, you create two "middle" terms, which in many cases are "like" terms and are then combined into one term. It is the creation of these "middle" terms which becomes the focus of this method of factoring a trinomial. This method is often called "split the middle" since it endeavors to create two "middle" terms which will make the factoring process easier. Once the middle is "split" into two parts, the process of "factoring by grouping" is used to arrive at the answer.
Since this factoring process starts by dealing with the leading coefficient, a, and the constant term, c, in the trinomial ax2 + bx + c, this method is also referred to as the "ac" method of factoring.
 |
"Split the Middle" Method for Factoring Trinomials ("ac" Method)
This "short cut" method gets the "Good Math Keeping" seal of approval. The steps in this process make rational mathematical sense, and the original expression is visibly maintained throughout the solution. |
|
The "ac" Method of Factoring Trinomials - "split the middle":
Factor a trinomial of the form ax2 + bx + c, a ≠ 1: |
Factor: 8x2 + 26x + 15 |
1. Always check for any common factors before you begin. |
There are no common factors in this trinomial. |
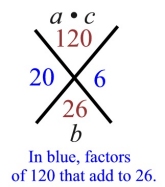
2. Find a • c (referred to as the Master Product). |
a • c = 8 • 15
= 120 |
3. Find two new numeric factors of a • c (120) that
will also add up to b (which is +26).
For this problem, these two new numeric factors will be 20 and 6.
These values of 20 and 6 will become the coefficients of the two new middle terms of the trinomial. |
Numeric factors of the value a • c,
20 • 6 = 120
that also add to b.
20 + 6 = 26
20 and 6 will now be the coefficients of 2 new middle terms |
4. Split the middle term into two terms using the sum of the two new factors, including the proper signs. The order of the middle terms does not matter. They will give the correct answer in either order. |
8x2 + 20x + 6x + 15
order of middle terms does not matter
Notice that this expression is equivalent to the original trinomial. |
5. Group the four terms to form two pairs. Be careful of the signs. (See example below for dealing with grouping a negative middle term.) |
(8x2 + 20x) + (6x + 15) |
6. Factor each pair by finding the common factors. |
4x(2x + 5) + 3(2x + 5) |
7. Factor out the common (shared) binomial. |
(2x + 5)(4x + 3) |
To get "Split the Middle" started, you need to find two numbers that multiply to a • c, and also add to the value of b. These two numbers will be used to form 2 new "middle terms", which will allow for "factoring by grouping" to arrive at the answer.
|
|
Visual Planner (using the Diamond Method): 
|
 |
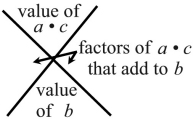| You may see a "visual planner" diagram, in the form of a large X, used to organize the numerical values in this "ac" Method of factoring. The two factors in the left and right corners of the X will be the coefficients of the two new "middle terms". |
Let's apply this visual planner to our previous example:
Factor: 8x2 + 26x + 15
In the top of the X, place the product of a = +8 and c = +15.
[8 • 15 = 120]
In the bottom of the X, place the value of b = +26.
Find the factors of 120 that will add up to 26, and place them in the right and left sections of the
X.
Possible factors of 120 are:
2 • 60
3 • 40
4 • 30
5 • 24
6 • 20 Stop!
6 + 20 = 26
Insert the two middle terms, using 20 and 6 as coefficients.
Group the sections and factor to arrive at the answer.
8x2+ 20x + 6x + 15
(8x2 + 20x) + (6x + 15)
4x(2x + 5) + 3(2x + 5)
(2x + 5)(4x + 3)ANSWER
|
 |
Dealing with negative values when using this "ac" Method.
1. Factor: 6 x2 + 13 x - 5
|
a • c = 6 • (-5) = -30 |
 |
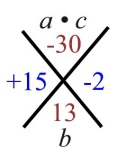(+15) • (-2) = -30
(+15) + (-2) = +13
These are the new factors that multiply to a•c (-30) and add to b (+13). |
6x2 + 15x - 2x - 5 |
(6x2 + 15x) - 1(2x + 5)
The safest way to "group" when the second middle term is negative is to factor out a -1 from the second pairing. Less errors are made with this approach. |
3x(2x + 5) -1(2x + 5)
|
(2x + 5)(3x - 1) Answer |
2. Factor: 2x2 - 13x + 21
|
a • c = 2 • 21 = 42 |
 |
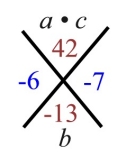(-6) • (-7) = 42
(-6) + (-7) = -13
These are the new factors that multiply to a•c (42) and add to b (-13). |
2x2 - 6x - 7x + 21 |
(2x2- 6x) - 1(7x - 21)
Again, the safest way to "group" when the second middle term is negative is to factor out a -1 from the second pairing. Less errors are made with this approach. |
2x(x - 3) - 1•7(x - 3)
2x(x - 3) - 7(x - 3) |
(x - 3)(2x - 7) Answer |
Mathematically speaking, why does this "short cut" method work?
The reason this method of creating two new "middle terms" works, is due to the relationships between the terms and their coefficients when two binomials are multiplied together.
Consider: (mx + n)•(px + q)
m, n, p, q are constants (numbers)
x is the variable
mpx2 +mqx + npx + nq
notice the two middle terms as a result of distribution
mpx2 +(mq + np)x + nq
factor out x from the two middle terms
The factored coefficient of the middle term is (mq + np).
The product of the coefficient of the first term and the constant is mp•nq.
NOTE: mp•nq is the product of numbers, so we can rearrange the order (or mq•np).
mq is a factor of mq•np
np is a factor of mq•np
The product of these two factors is mq•np
The terms that create the sum for the middle term (mq and np)
are factors of the product of the coefficient of the first term and the constant (mq • np).
(mpx2 +mqx) + (npx + nq)
split the middle, and group
mx(px + q) + n(px + q)
factor by grouping
(mx + n)•(px + q)
distributive property in reverse
The results from factoring by grouping give us that with which we started.
