A circle is a conic section. It is a slice of a right cone parallel to the circular base of the cone.
In this section, we will be examining this "circular slice" as to its properties and equations in relation to the coordinate plane.
|
A circle is defined as the set (locus) of points in a plane equidistant from a given point (the center of
the circle.)
|
|
 Circle with Center at Origin (0,0) Circle with Center at Origin (0,0)
x2 + y2 = r2
with the center at (0,0)
and the radius r |
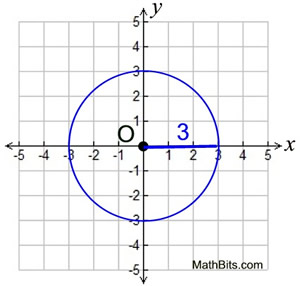
In the example at the right, x2 + y2 = 9.
The center is (0,0) and the radius = 3.
|
 |
 Circle with Center at Point (h, k)
(Known as "center-radius form" or "standard form".) Circle with Center at Point (h, k)
(Known as "center-radius form" or "standard form".)
(x - h)2 + (y - k)2 = r2
with the center at (h, k)
and the radius r |
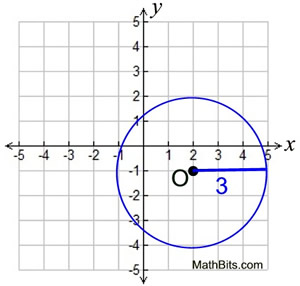
In the example at the right,
the center is (2,-1) and the radius = 3.
(x - 2)2 + (y - (-1))2 = 9
(x - 2)2 + (y + 1)2 = 9.
|
 |
|
Did you notice that the formula for the circle with the center at the origin is just a special case of the formula for a circle at point (h,k)?
When h = 0 and k = 0 (for the center at the origin), the formula becomes
(x - h)2 + (y - k)2 = r2
(x - 0)2 + (y - 0)2 = r2
x2 + y2 = r2
|
|
 General Form
If we "multiply out", the center-radius form, we obtain the "general form" of the equation of a circle. Notice that in this form, we can clearly see that the equation of a circle has both x2 and y2 terms and these terms have the same coefficient (usually 1, but not always). General Form
If we "multiply out", the center-radius form, we obtain the "general form" of the equation of a circle. Notice that in this form, we can clearly see that the equation of a circle has both x2 and y2 terms and these terms have the same coefficient (usually 1, but not always). |
|
|
 Derivation of the Circle Formula Derivation of the Circle Formula
With a little help from the Pythagorean Theorem, we can easily verify the circle equation formulas.
The diagram at the right shows a circle with center (h,k) and a right triangle with hypotenuse r.
The sides of the right triangle can be expressed
as (y - k) and (x - h).
Applying the Pythagorean Theorem, we have:
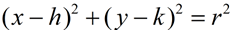
which is the Center-Radius Form of the equation of a circle. |
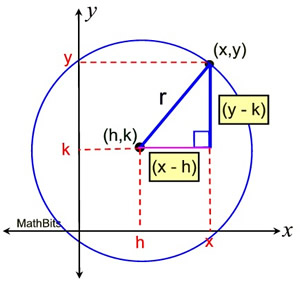 Circle with center (h,k).
Circle with center (h,k).
Draw a right Δ with hypotenuse r. |
 Write the equation of a circle with center at (4,8) and a radius of 12. Write the equation of a circle with center at (4,8) and a radius of 12.
ANSWER:
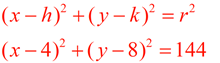
 Given the equation of a circle, (x + 4)2 + (y - 5)2 = 50, find the coordinates of the center and the radius. Given the equation of a circle, (x + 4)2 + (y - 5)2 = 50, find the coordinates of the center and the radius.
ANSWER:
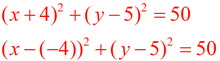 Remember that a + sign inside the parentheses means that the coordinate will be a negative value.
The center is (-4,5) and
Remember that a + sign inside the parentheses means that the coordinate will be a negative value.
The center is (-4,5) and
the radius is 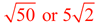 . . |
Notice that the answer for the radius is left in radical form. Do not estimate (round) an answer unless told to do so, or unless working in a real world measurement situation. It is hard to measure a radical number of feet. |
|
 Convert x2 + y2 - 4x - 6y + 8 = 0 into center-radius form. Convert x2 + y2 - 4x - 6y + 8 = 0 into center-radius form.
When given the "general form", it will be necessary to covert the equation into the center-radius form to determine the center and the radius and to graph the circle. To accomplish this conversion, you will need to "complete the square" on the equation. You have worked with completing the square in the past. If you need a quick refresher, see the Completing the Square Refresher page.
We will be creating two perfect square trinomials within the equation.
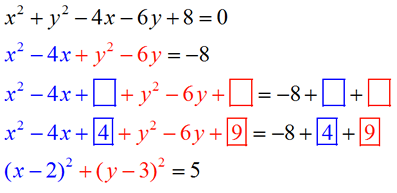
The center of this circle is at (2,3)
and the radius is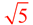 . . |
• Start by grouping the x-related terms together and the y-related terms together. Move any numerical constants (plain numbers) to the other side.
• Get ready to insert the needed values for creating perfect square trinomials. Remember to balance both sides of the equation.
• Find the missing value by taking half of the "middle term" (the linear coefficient) of the trinomial and squaring it. This value will always be positive as a result of the squaring process.
• Rewrite in factored form.
|
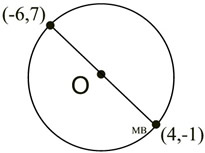
 Write the equation of a circle whose diameter has endpoints Write the equation of a circle whose diameter has endpoints
(4,-1) and (-6,7).
| |
Find the center of the circle by using the midpoint formula.
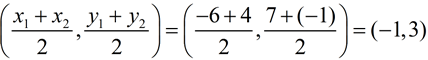
Find the radius by using the distance formula.
Note: we are using the center (-1,3).
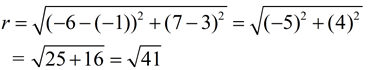
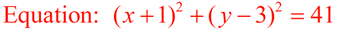
|
 |
 Write the equation for the circle x2 + y2 = 16, if its center is translated by (x, y)→(x + 6, y - 3). Write the equation for the circle x2 + y2 = 16, if its center is translated by (x, y)→(x + 6, y - 3).
ANSWER: The center of the given circle is at the origin. The translated center will be shifted 6 units to the right and 3 units down, placing it at (6,-3). The circle has a radius of 4. The equation will be (x - 6)2 + (y + 3)2 = 16.
 For the circle
2x2 + 2y2 + 6x - 8y + 12 = 0, find the center and radius. For the circle
2x2 + 2y2 + 6x - 8y + 12 = 0, find the center and radius.
Whoa! We haven't seen an equation like this before.
Is this equation even a circle?
In this equation, both the x and y terms appear in a squared form and their coefficients have the same sign and are equal. Yes! This equation is a circle. We will, however, have to deal with the coefficients of 2 before we complete the square.
|
|
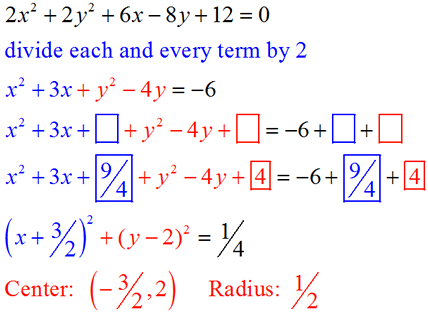 |
• Divide through by 2.
• Group the terms.
• Get ready to create perfect squares.
• Take half of the "middle term" of the trinomial and square it.
• Factor and write in center-radius form. |
|