A conic section (or just "conic") is a curve obtained by the intersection of a plane with a right circular cone. When a plane "slices" through the cone, at various angles and locations, the outline of the surface of the slice becomes a two-dimensional representation of a mathematical curve.
Conic sections are known as quadratic relations (not functions) since their equations are of second order but are not always functions.
The four basic conic sections are circle, parabola, ellipse and hyperbola.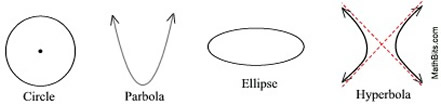
In Geometry, we will concentrate on the circle and the parabola.
(Let the sword represent the plane slicing through the cone.)
Circle:
The circle is obtained when the cutting plane (represented by the sword) is parallel to the base of a right cone. The cutting line is perpendicular to the symmetric axis of the cone and creates a closed curve.
The word "circle" is Greek meaning "hoop" or "ring". The circle has been know since before the beginning of recorded history, in the form of natural circles.
A circle is the set (locus) of points in a plane equidistant from a given point (the center).
Equations:
x2 + y2 = r2 (center at origin)
(x - h)2 + (y - k)2 = r2 (center at (h,k) Standard Form)
x2 + y2 + Cx + Dy + E = 0 (General Form)
A conic section is a circle when the x2 and y2 terms have the same sign and equal coefficients. A circle is a quadratic relation (not a function). |
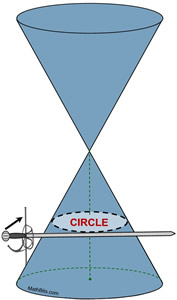
This is called a double-napped cone, and is used when studying conic sections. |
Parabola:
The parabola is obtained when the cutting plane, represented by the sword, is parallel to one side (the generating line) of the cone. The conic, a parabola, is an unbounded curve.
The word "parabola" is Greek for a two-dimensional, mirror-symmetrical curve.
A parabola is the set (locus) of points in a plane that are equidistant from both the directrix (a fixed straight line) and the focus (a fixed point).
Equations:
y = x2
y = ax2 + bx + c (Standard Form)
y = a(x - h)2 + k (Vertex Form)
(y - k)2 = 4p(x - h) with focus at (h+p,k) and directrix x = h - p
x = ay2 + by + c (horizontal parabola), also (x - h)2 = 4p(y - k)
A parabola has an equation that contains only one squared term. If the parabola contains ± x2, the graph opens in a y-direction (vertically up or down) and is a function. If the parabola contains ± y2, the graph opens in an x-direction (horizontally left or right) and is a quadratic relation (not a function.) |
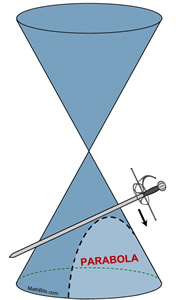 |
History:
The conic sections have been studied since 200 BC. The earliest definition differed somewhat from what is used today and did not include the circle. While the circle may still be considered a special case of the ellipse, it is often referred to as the "fourth" conic section due to its mathematical significance.
It was Rene Descartes (1596-1650) that applied Analytic Geometry (with his Cartesian coordinate system) to the study of conics, allowing for these geometric shapes to be expressed as algebraic equations.
Conic sections have applications in astronomy (orbits of planets), paleontology (the study of fossils), physics (trajectory, parabolic reflectors), architecture (suspension bridges), music (reflecting sound), aircraft (zero gravity), highway design (vertical curves) to name only a few. |