Example 1: Campers are starting to gather for the evening campfire sing-a-long. Each camper is instructed to sit approximately 5 feet from the center of the fire. As more campers gather, what geometric shape, or path, represents this seating pattern?
ANSWER: a circle, center P, radius 5 feet
Set of points: the campers' locations
Condition: 5 feet from the fire's center
Locus: a circle |
|
The path where the campers are sitting is a "locus". You see a set of points (campers), all doing the same thing, to form a pattern (a circle). While the formal statement of this theorem may sound confusing, it actually represents a concept that you already know and understand.
|
Example 2: While her pasture fence was being repaired, Esmeralda, the goat, was temporarily tied to a stake in the ground. Her rope, attached to the stake, was 18 feet long. If Esmeralda walks at the end of her rope, what is the locus of her path?
ANSWER: a circle, center stake, radius 18 ft.
Set of points: the goat's locations
Condition: 18 feet from the stake
Locus: a circle
|
 |
Let's see how this situation sounds when worded to follow the theorem: The locus at a distance of 18 feet from point P (the stake), is a circle with a center at P and a radius, d, of 18 feet.
|
Example 3: Declan wants to buy a set of retro tires for a vehicle he is restoring. He notices that the seller has placed a red identification dot on the tread of each tire. If Declan spins the tire while the tire is off the ground, what is the path of the red dot?
ANSWER: a circle, center at center of tire, radius half diameter of the tire.
Set of points: the red dot's locations
Condition: constant distance from tire center
Locus: a circle |
|
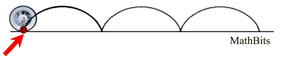
 When Declan puts the tire on his vehicle, and the tire rolls along the road, the red dot will not travel in a circle in relation to its contact with the surface of the road. When a fixed point on a circle (such as the red dot) rolls on a line (such as along the road), it forms a curve called a cycloid.
|
|