|
A locus is the set of all points which satisfies a certain condition. |
The term "locus" has been known to strike fear in the hearts of many geometry students.
But don't panic! Simply replace the word "locus" with the words "set of points" and read the question again.
 |
The time-lapsed photograph at the left shows the headlights and taillights of vehicles as they drive along the road.
The photo shows the set of points (locus) of the headlights (or taillights) as traced under the condition that the vehicles follow the path of the roadway.
Set of points: the headlight's locations as seen in the photo
Condition: following the road
Locus: the lanes (paths) in the roads, as shown in the picture
Think of a locus as a "bunch" of points that all do the same thing. |
In Latin, the word locus means place. The plural of locus is loci.
A locus is usually drawn using dashes. |
There are six locus theorems (rules) that are popular in geometry.
Due to their connections to equal distances, parallel lines, and angle bisectors, questions pertaining to these locus theorems may also contain a construction component. While these theorems may sound confusing at first reading, their concepts are actually very easy to understand. Don't panic!
Locus Theorem 1:
The locus at a fixed distance, d, from point P is a circle with the given point P as its center and d as its radius.
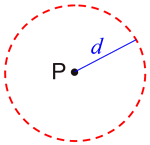
This theorem asks you to "describe the path formed by all points located the same distance from 1 point".
ANSWER: The path will be a circle. |
Locus Theorem 2:
The locus at a fixed distance, d, from a line m, is a pair of parallel lines at a distance of d from line m, and located on either side of m.
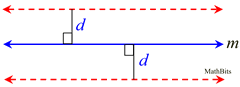
This theorem asks you to "describe the path formed by all points located the same distance from 1 line".
ANSWER: The path will be 2 lines; one on each side of the given line.
|
Locus Theorem 3:
The locus equidistant from two points A and B, is the perpendicular bisector of the line segment joining the two points.
(Sound familiar?)
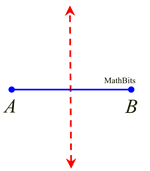 This theorem asks you to "describe the path formed by all points located the same distance from A as from B".
This theorem asks you to "describe the path formed by all points located the same distance from A as from B".
ANSWER: The path will be the perpendicular bisector of 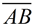 . . |
Locus Theorem 4:
The locus equidistant from two parallel lines, m1 and m2, is a line parallel to both m1 and m2 and halfway between them.
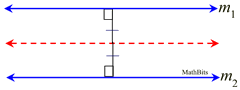
This theorem asks you to "describe the path formed by all points the same distance from two parallel lines".
ANSWER: The path will be 1 line halfway between the parallel lines. |
Locus Theorem 5:
The locus in the interior of an angle equidistant from the sides of the angle is the bisector of the angle (exclusive of the vertex).
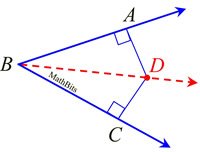
This theorem asks you to "describe the path formed by all points the same distance from both sides of an angle".
ANSWER: The path will be the angle bisector. |
Locus Theorem 6:
The locus equidistant from two intersecting lines, m1 and m2, is the pair of lines which bisect the angles formed by the lines m1 and m2.
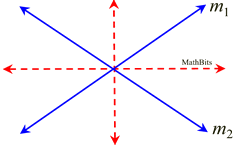
This theorem asks you to "describe the path formed by all points located the same distance from 2 intersecting lines".
ANSWER: The path will be a pair of lines which bisect the angles formed. |
Strategy for Solving Locus Problems: |
1. Draw a diagram using the given information.
2. Read carefully to determine what conditions need to be satisfied.
3. Start by finding ONE point that satisfies the needed conditions and plot it on your diagram. Then find several additional points that satisfy the conditions and plot them as well. Continue plotting points until you can see the pattern, or path, that is developing.
4. Draw a dashed line, or circle, through the plotted points to show the locus.
5. If you are asked to describe your locus in writing, be very specific so you will give a clear description of your work.
6. If TWO, or more, conditions exist in the problem (a compound locus), repeat steps 2 through 5 for the additional conditions on the same diagram. You will know you have a compound locus when you see the words "AND" or "AND ALSO" separating the conditions.
7. For a compound locus, count the number of locations where the two loci intersect (where the dashed drawings cross). Clearly label these locations on the diagram, or describe them in words.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|







