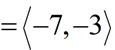|
A translation "slides" an object a fixed distance
in a given direction.
You can think of a translation as
sliding, or pushing, an object in one direction.
The original object and its translation have the
same shape and size, and they face in the same direction.
The object is not turned nor flipped.
The word "translate" in Latin means "carried across."
|
 |
 |
Translations are SLIDES!! |
|
Translations can be seen, in a variety of situations:
|
(←) Translations can be seen in nature. The hexagonal sections of a honeycomb are the same size, the same shape and face in the same direction.
|
| |
(→) As you go down a slide, you are undergoing a translation. You are moving a given distance in a given direction. You do not change your size, shape or the direction in which you are facing (hopefully!). |
|
|
Certain patterns of musical notes are often repeated (translated) within a composition.
|
The artist M. C. Escher continually used translations, reflections, and rotations in his famous art works. To see the works of M. C. Escher, visit
http://www.mcescher.com. |
Seats in a stadium are the same size, the same shape, and face in the same direction. |
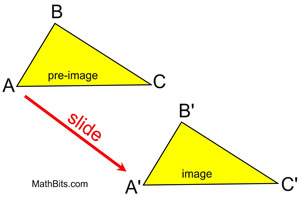
A translation moves ("slides") an object a fixed distance in a given direction without changing its size or shape, and without turning it or flipping it.
• The original object is called the pre-image, and the translation is called the image.
• The image is usually labeled using a prime symbol, such as A'B'C'.
• Translations may be described by their movement, such as 5 units to the right and 2 units down.
|
 |
• An object and its translation have the same shape and size, and face in the same direction.
• A translation creates a figure that is congruent with the original figure, and is referred to as a rigid transformation.
•
Naming (lettering) a figure in a translation occurs in the same direction in both figures (such as both clockwise or both counterclockwise).
Properties preserved under a translation
from the pre-image to the image:
1. distance (lengths of segments remain the same)
2. angle measures (remain the same)
3. parallelism (parallel lines remain parallel)
4. collinearity (points remain on the same lines)
5. midpoints (midpoints remain the same in each figure)
6. orientation (lettering order remains the same) |
|
 The preserved properties of a transformation are referred to as being "invariant" in that they do not vary (change) during the transformation.
|
|
Translations in the coordinate plane:
 Translation 6 units right:
 |
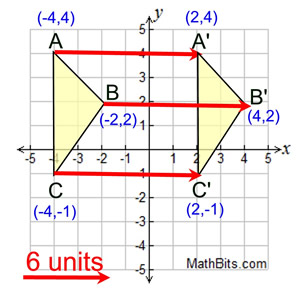Notice how each vertex moves the same distance in the same direction. All three vertices (A, B and C) are moved 6 units horizontally to the right.
If you move horizontally 6 units to the right, 6 is added to the x-coordinate of each of the vertices. The distance you move horizontally to the "right" gets "added" to the x-coordinate.
Translation 6 units to the right.
(x, y) → (x + 6, y) |
|
6 units left, 3 units up:
 |
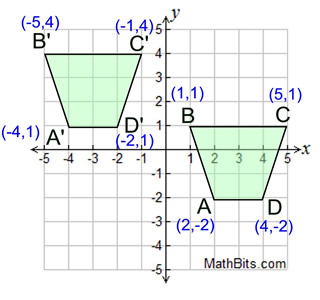Be sure you notice where the original figure, ABCD, is located. In this graph, ABCD is on the right. The trapezoid is sliding to its left and up.
Each vertex of ABCD is moved 6 units to the left, and then 3 units up. The distance you slide horizontally to the "left" gets "subtracted"
from the x-coordinate, and the distance you slide "up" gets "added" to the y-coordinate.
Translation 6 units left and 3 units up.
(x, y) → (x - 6, y + 3) |
|
Translations:
When sliding ...
• horizontal to the right - add distance to x-coordinate
• horizontal to the left - subtract distance from the x-coordinate
When sliding ...
• vertical up - add distance to the y-coordinate
• vertical down - subtract distance from the y-coordinate |
There are several ways to indicate that a translation is occurring:
1. description:
|
Description notation:
A verbal or written description of the translation can be given.
Example: "8 units to the right and 6 units down."
|
2. mapping:
|
Mapping notation.
Example:
(x, y) → (x + 8, y - 6)
Read: "the x and y coordinates are mapped to x + 8 and y - 6 respectively". (Notice that adding a negative value (subtraction), moves the image left and/or down, while adding a positive value moves the image right and/or up.)
|
3. notations:
|
Translation notation:
Example: T8,-6
or T8,-6 (x, y) = (x + 8, y - 6)
The 8 tells you to "add 8" to all x-coordinates, while the -6 tells you to "subtract 6" from all of the y-coordinates.
|
| 4. vectors: |
Vector notation:
Example: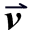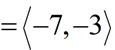  
A vector, a directed line segment, may also be used to show the movement of a translation.
See more about vectors and translations.
|
A translation (notation Ta,b ) is a transformation that
slides every point of a figure the same distance in the same direction.
Ta,b (x,y) = (x + a, y + b)
|
EXAMPLE:
The diagram at the left shows a translation of ΔABC.
description: ΔABC has been moved 4 units to the right and 9 units down
mapping: (x, y) → (x + 4, y - 9)
notation: T4,-9
T4,-9 (x, y) = (x + 4, y - 9)
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
