|
These are general terms that you will see in your study of transformations.
Remember that transformations are operations that alter the form and/or location of a figure.
The standard transformations are reflections, translations, rotations, and dilations.
Terms are listed in alphabetical order.
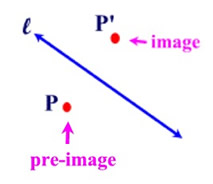
| Image: An image is the resulting point or set of points under a transformation. For example, if the reflection of point P in line l is P' (referred to as P prime), then P' is called the image of point P under the reflection (of the pre-image). Such a transformation is denoted rl (P) = P'. |
 |
Isometry: An isometry is a transformation of the plane that preserves length. For example, if the sides of an original pre-image triangle measure 3, 4, and 5, and the sides of its image after a transformation also measure 3, 4, and 5, the transformation has preserved length.
A direct isometry preserves orientation or order - the letters on the diagram go in the same clockwise or counterclockwise direction on the figure and its image.
A non-direct or opposite isometry changes the order (such as clockwise changes to counterclockwise).
|
|
|
| Invariant: A figure or property that remains unchanged under a transformation of the plane is referred to as invariant (not varying). It means no variations in the figure have occurred. |
Opposite Transformation: An opposite transformation is a transformation that changes the orientation of a figure. Reflections and glide reflections are opposite
transformations.
|
For example, the original image, triangle ABC, has a clockwise orientation - the letters A, B and C are read in a clockwise direction. After the reflection in the x-axis, the image triangle A'B'C' has a counterclockwise orientation - the letters A', B', and C' are read in a counterclockwise direction.
A reflection is an opposite transformation. |
|
Orientation: Orientation refers to the arrangement of points, relative to one another, after a transformation has occurred. For example, reference made to the direction traversed (clockwise or counterclockwise) when traveling around a geometric figure is its orientation. The "lettering" of the vertices may appear in the same order, or in reverse order, around the figure.
|
|
|
The reflection at the left, shows the original image, triangle ABC, with clockwise lettering (orientation) A, B and C in a clockwise direction. After the reflection in the x-axis, the image triangle A'B'C' has a counterclockwise orientation - the letters A', B', and C' are read in a counterclockwise direction. |
| Position Vector: A position vector is a coordinate vector whose initial point is the origin. Any vector can be expressed as an equivalent position vector by translating the vector so that it originates at the origin. |
| Rigid Transformation: A rigid transformation (or isometry) is a transformation of the plane that preserves length (distance). For example, if the sides of an original pre-image triangle measure 3, 4, and 5, and the sides of its image after a transformation measure 3, 4, and 5, the transformation preserved length. |
Transformation: A transformation of the plane is a one-to-one mapping (or moving) of points in the plane to points in the plane. In the plane, a mapping will carry ordered pairs to new locations according to some specified rule. |
Transformational Geometry: Transformational Geometry is a method for studying geometry that illustrates congruence and similarity by the use of transformations. |
Vector: A vector is a quantity that has both magnitude and direction; represented geometrically by a directed line segment. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|