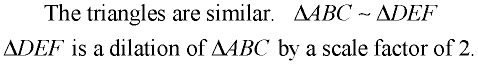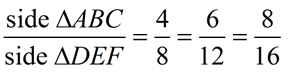|
Similar figures are figures with the same shape, but not necessarily the same size.
The term similar (or similarity) can be defined using the language of transformations.
Transformations |
Two figures are similar if and only if one figure can be obtained from the other by a single transformation , or a sequence of transformations, including translations, reflections, rotations and/or dilations. |
|
Two figures are similar if one is the image of the other under a transformation
that multiplies all distances (lengths) by the same positive scale factor.
That is to say, one figure
is a dilation of the other.
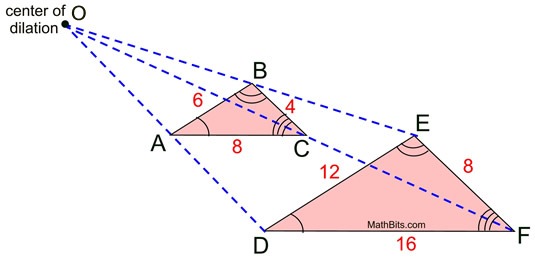
ΔDEF is a dilation of
ΔABC by a scale factor of 2.
OD = 2•OA
OE = 2•OB
OF = 2•OC
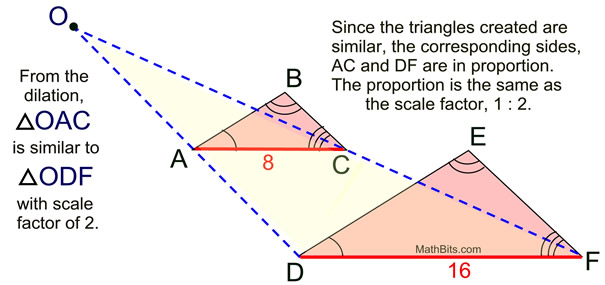
You will learn in high school Geometry that there are additional methods for proving triangles similar
using proportional sides and angles. Such methods were used to verifty that the dilation formed triangles shown above are similar. It was not AA that was used.
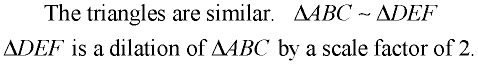
The lengths of the sides of
ΔDEF are twice the lengths of the sides of ΔABC.
Or, ΔABC is a dilation of
ΔDEF by a scale factor of ½.
The lengths of the sides of
ΔABC are half the lengths of the sides of ΔDEF.
Remember that in similar triangles, the corresponding sides are in proprotion.
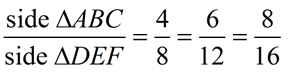
Can you see the dilation at work in these ratios?
We now have, rigid transformations and similarity transformations.
 A similarity transformation is a transformation in which the image has the same shape as the pre-image.
The study of rigid transformations (isometries) showed a connection between congruent figures and the transformations of types called translations, reflections, and rotations. Rigid transformations preserve size and shape.
|
Rigid Transformations
Translations
Reflections
Rotations
"same shape and same size"
(congruent) |
Similarity Transformations
Translations
Reflections
Rotations
Dilations
"same shape"
(similar) |
|
Similarity transformations also include translations, reflections, and rotations, with the addition of dilations. Similarity transformations preserve shape, but not necessarily size, making the figures "similar". Since it is possible for similar figures to have a scale factor of 1 (making the shapes the same size), it can be said that all congruent figures are also similar. Keep in mind, however, that most similar figures do not preserve size.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
