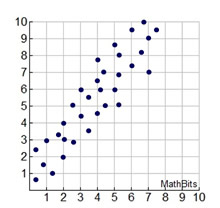
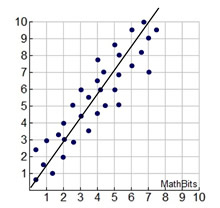
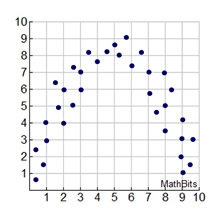
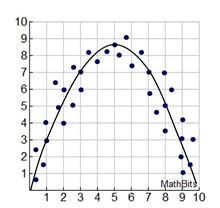
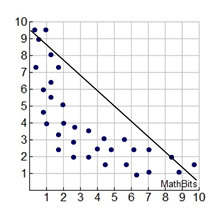
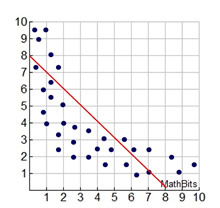
We have seen how data can often be represented by a stratight line (linear association).
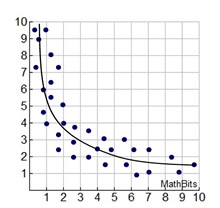
Sometimes, however, a "straight line" is not the best shape to represent the data.
There are actually, different types of "curves" that can be used
to model data, referred to as non-linear associations.

Non-linear Scatter Plots
Plots that DO NOT resemble a straight line.
For this level course, you should be able to describe
a pattern as non-linear by looking at the scatter plot.

 stump
Linear:

dataline1

This scatter plot forms a straight line. The points are rising from left to right across the graph in a linear manner.

dataline2

A line can be drawn with approximately the same number of dots above and below the line.
Obviously non-Linear:

dataparabola2

This scatter plot clearly does not form a straight line. First the dots go up, but then they turn and go back down.

dataparabola1

While a "line" of best fit is not possible with this scatter plot, it may be possible to draw a "curve" of best fit.
Not Obviously non-Linear:

dataexp2

It is not easy to determine whether this scatter plot is linear or not, but it is non-linear. See *Hint below.

dataexp1

A curve can be fitted to this data with approximately the same number of dots above and below the curve.

* Hint:
Let's examine that last scatter plot (from above) again.
What if we think it is linear?

If you draw a line on a curved scatter plot and the dots collect in mass only on one side of the line for a portion of the graph, the scatter plot is mostly likely non-linear.
datalineblack

Notice how a group of the dots are only to the left (or below) the line for a section of the graph.. CLUE: This is non-linear.
datalinered

Even if we move the line to a new
position, we still have a mass of the
dots on one side of the line only.

beware It may not always be obvious from looking at a scatter plot which shape (curve) will be the best fit. For a "curve of best fit" we still try to keep the same number (or approximately the same number) of dots above the curve as below the curve, as we did with a "line of best fit".

Some situations may require more investigation before deciding upon a possible shape (curve), and some situations may not be modeled by any specific shapes (curves). Finding a "line of best fit" by hand is possible, but finding a "curve of best fit" is much more difficult. So, it upcoming courses, we will call for help from our graphing calculator to assist with "curves of best fit".


divider


NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".