 Integers are the numbers that fit into a set, Integers are the numbers that fit into a set, 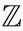 , that looks like: , that looks like:
{. . . , -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, . . .} |
 Integers are made up of : Integers are made up of :
1. the positive integers, which are the natural numbers (the counting numbers, 1, 2, 3, ...)
2. the number zero (zero is neutral, neither positive nor negative)
3. the negative integers, which are the opposites of the natural numbers (also known as additive inverses)
Note: There are no fractions nor decimal values in the set of Integers.
(This excludes the equivalence of denominators of 1 and decimals of "decimal point 0"),
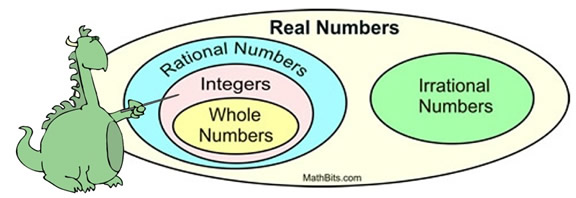
 Where are Integers in the Number System? Where are Integers in the Number System?
The Integers contain the set of Whole Numbers {0, 1, 2, 3, 4, 5, 6, ...} (which contains the set of Natural Numbers {1, 2, 3, 4, 5, 6, ...}), along with the opposites of the Natural Numbers.
 Opposites: Opposites:
| Two numbers are opposites if they are the same distance away from zero on the number line, and are on "opposite" sides of the zero. |
One number will be a positive integer, on the right side of the number line, with a positive (+) sign, which is implied but not always written. The other number will be a negative integer, on the left side of the number line, with a negative (-) sign which is always written.
For example, +5 and -5 are opposites.
This concept of "opposite" is also referred to as an additive inverse.
An additive inverse is a number that when added to a given number gives zero as the result. The additive inverse of +5 is -5.
In plain English, additive inverses will have the same numeric entry, but with different signs (one a plus sign, one a negative sign).
|
Additive Inverses:
5 + -5 = 0
-5 + 5 = 0 |
|
The concept of "opposites" applies to all Real Numbers,
including Integers and Rational Numbers. |

 Opposites in Real-World Situations: Opposites in Real-World Situations:
Due to their positive and negative nature, integers are often used to describe real-world situations. For example, when dealing with above zero and below zero temperatures, positive or negative "signed" numbers can be used to represent these conditions.
Note: The term "signed numbers" refers to positive and negative numbers, in general. Signed numbers may be Integer, Rational, or Real numbers.
See "Signed Numbers and Opposites" for examples of real-world situations.

 Things to Remember about Integers: Things to Remember about Integers:
• In the vertical number line at the right, 6 and -6 are opposites.
They are the same distance from zero.
• In the vertical number line at the right, 3 and -3 are opposites.
-3 + 3 = 0
Ordering is arranging numbers from least to greatest,
or from greatest to least. Inequality signs may be used.
On a horizontal number lines (like above),
the farther right you go, the greater the number.
On vertical number lines, (like at right),
the farther up you go, the greater the number.
• Order: 6 > -6 or -6 < 6
• Order: 3 > -3 or -3 < 3
• Order: 6 > 3 or 3 < 6
• Order: -3 > -6 or -6 < -3
 • 0 is its own opposite. • 0 is its own opposite.
 •
The opposite of the opposite of a number is the number itself. •
The opposite of the opposite of a number is the number itself.
 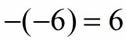
Two negatives make a positive in this case. |
|
The concept of "ordering" applies to all Real Numbers,
including Integers and Rational Numbers. |

* Vertical number lines may give you a clearer view of the order of the numbers (that is, how they compare to one another in size).
The higher up the number line you go,
the greater the number.
Remember that a vertical number line looks like a thermometer, where the temperatures increase (get larger) as you read up the thermometer.
On a vertical number line,
it is easy to see that
50º F is colder than 64º F,
and that
-10º F is warmer than -20º F.
|
  |
|
|