 The absolute value of a number is the distance
between the number and zero on the real number line.
The notation used for absolute value is two vertical bars.
You may also see the notation "abs( )", such as abs(−5) = 5.
Calculators like to use this abs( ) notation.
|
| -4 | = 4 means that -4
is 4 units from zero.
| 5 | = 5 means that 5
is 5 units from zero.
The absolute value of 0 is 0.
| 0 | = 0
... because 0 is 0 units away from itself. |
Distances are measured as positive units (or zero units).
Consequently, absolute value is never negative.
Taking the absolute value of any number,
returns a positive number, or zero.
Absolute value answers the question "How far from zero?",
but not the question "In which direction from zero?".
Note: The additive inverse of | -6 | is -6. Since | -6 | = 6, the additive inverse is -6.
Absolute value also deals with the distance between values
on the number line.
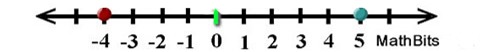
What is the distance between -4 and 5?
Given two values on a horizontal or vertical number line,
the distance between the points is the absolute value of the difference of the points.
| -4 - 5 | = 9 and also | 5 - -4 | = 9
It does not matter which point is used first in the subtraction.
We can verify that this is the correct result by counting the spaces between -4 and 5 on the number line.
The distance on a number line between values a and b is
| a - b | or | b - a |. |
Absolute value can also be involved in mathematical computations.
Absolute value should be treated as a grouping symbol in the order of operations.
Be sure to evaluate, or simplify, any values within the absolute value before evaluating the absolute value.
For example: | 4 − 6 | = | −2 | = 2 and | 6 − 4 | = | 2 | = 2
Considerations to keep in mind when working with absolute value:
NOTE: When working with absolute value within a problem, be sure to deal with the absolute value first, before proceeding with the solution. |
1. − | −7 | = −7
In the expression − | −7 |, replace | −7 | with 7 before continuing. Thus the result is −7.
While
− ( −7 ) = +7, the idea of "two negatives making a positive" does not apply with the absolute value in this problem. |
2. | −4 x 5 | = | −20 | = 20
As shown, deal with the inside of the absolute value first, then finish the problem. |
3. | −3 | x | −3 | = 3 x 3 = 9
Again, deal with the absolute value first. |
4. | 3 | + | − 7 | − | − 2 | = 8
3 + 7 − 2 = 8
Deal with all three of the absolute value expressions first, then use your knowledge of integers to finish the problem. |
5. | − 8 | + ( − 9) + | − 14 | + ( − 2) = 11
8 + (−9) + 14 + (−2)
−1 + 14 + (−2)
13 + (−2)
11
Be careful in this problem. Only two of the four terms deal with absolute value. Do not confuse absolute value with parentheses. |
6. | − 6 | ÷ | − 2| = 3
| − 6 | = 6 and | − 2 | = 2
6 ÷ 2 = 3 |
7. Consider the following situation:
• Last week your checking account had a negative balance (-$850).
You were in debt and owed the bank $850.
• You write another check for $50.
• The bank calls you and tells you that your balance is now $50 less than your previous
balance.
• How much do you owe the bank? ANS: $850 + $50 = $900
The moral of the story?
"An account balance less than a negative amount represents a debt greater than the absolute value of that amount."
Sounds impressive, doesn't it!
|
|
For help with absolute value
on your calculator,
click here. |
|
|
|
