"I am traveling at a high rate of speed!!
I'm going 5m inches per minute where m equals 10.
So, at what rate of speed is this little ant
actually traveling in this matchbox cruiser?
Answer: 50 inches per minute
|
 |
A rate is a ratio that compares two different kinds of numbers, such as miles per hour, or inches per second. A unit rate compares a quantity to its unit of measure. |
A rate can express how long it takes to do something.
To drive 50 inches in one minute is to drive at the
rate
of 50 in./min.
This fraction (50/1) expressing the rate has units of distance
in the numerator and units of time in the denominator.
When the denominator of the "rate" fraction is a "single unit of one" (such as 1 minute), the rate is referred to as a unit rate. The most common type of rate is "per unit of time",
such as "miles per hour" or "inches per minute". |
When working with rate, the words "per, for and each" are often used to separate the units. |
Symbols such as / or @ may be used when discussing rates. |
Unit rate - a rate with a denominator of 1. |
|
Other Ways to Look at Rates
Rates
• A rate is a ratio in which the two measurements have different units.
• A rate refers to the frequency by which an event happens.
• A rate refers to the changes in measurements or units. |
 |
• Rates are most often expressed in "per unit" form with a denominator of 1.
Examples: 55 mph; $15 per hour; 350 calories per serving. |
|
Solving a problem dealing with rate may involve dealing with a proportion.
Situation: The ant's cruiser is powered by sugar water. If the cruiser goes 125 inches per tablespoon of sugar water, how far can it go on 5 tablespoons of sugar water?
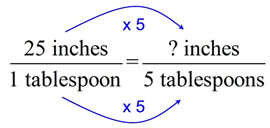 |
The equation at the left shows two ratios being equal. This equation is called a proportion.
To solve, observe that the bottom values changed by a multiple of 5. Do the same to the top values. 25 x 5 = 125. ANSWER: 125 inches. |

 |
Find the unit rate: The ant's cousin has a bigger matchbox cruiser that travels at a rate of 150 inches in 2 minutes. What is the unit rate traveled by this crusier? |
Solution:
To find the unit rate, the denominator needs to be 1.
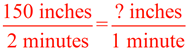 |
Method 1:
Observe that 2 minutes changing
to 1 minute is division by 2.
Do the same to the top:
150 divided by 2 = 75
Answer:
75 inches per 1 minute.
Or just 75 inches per minute.
To get unit rate, simply divide:
150 ÷ 2 = 75
|
Method 2: (More advanced method)
Use "cross multiply" (in a proportion, the product of the means equals the product of the extremes) to solve.
2x =1350
x = 75
Answer:
The unit rate is 75 inches per minute. |
|
|
 |
Find a missing term given rate: How long, in minutes, did it take the ant to cover 350 inches at a rate of 50 inches per minute? |
Solution:
Set up a proportion:
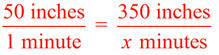
|
Method 1:
Observe that 50 inches changing to 350 inches is a multiple of 7.
Do the same to the denominator: 1 times 7 = 7.
Answer 7 minutes. |
Method 2: (A more advanced method.)
Use "cross multiply" (in a proportion, the product of the means equals the product of the extremes) to solve.
50x = 350
x = 7
Answer: 7 minutes |
|
|
 |
Comparing unit rates: The sugar water fuel for the ant cruiser is sold in two different sizes. A 12 tablespoon container costs $0.62. A 8 tablespoon container costs $0.45. Which is the better buy? |
Solution:
Convert each pricing to its unit rate ( 1 tablespoon) by using division.
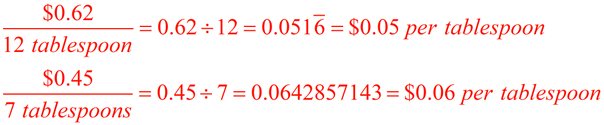
The unit rate that is smaller (that costs less) is the better value.
ANSWER: Purchasing the container with 12 tablespoons of fuel is the better buy. |
|
|
 |
Distance = Rate x Time: The ant drives his matchbox cruiser from his home to his friend's house traveling at the rate of 50 inches per minute. He then walks back to his home at the rate of 10 inches per minute. If the round trip took 9 minutes, how far is it from the ant's home to his friend's house? |
Solution:
Let t = cruiser time
9 - t = walking time
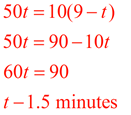 |
Distance = Rate x Time
The distance driving the cruiser to the friend's house is the same distance that the ant walks back home = round trip. Hint: We need to first find the "time" which can then be used to find the "distance".
Answer: Distance = 50(t) = 50(1.5) = 75 inches
As a check: 10(9 - t) = 10(9 - 1.5) - 10(7.5) = 75 inches.
The round-trip is the same distance in both directions.
|
|
|
|