This lesson is going to take a "quick look" at adding, subtracting, multiplying and dividing square roots. For more information regarding these operations, refer to the Radical Section under Algebra 1.
Adding or subtracting radicals is the same concept as that of adding or subtracting similar, or "like", terms. The index and the values under the radical (the radicands) must be the SAME (creating "like radicals") before you can add or subtract the radical expressions.
|
Adding and subtracting radicals: For radicals having the same index and the same values under the radical (the radicands), add (or subtract) the values directly in front of the radicals and keep the radical. |
|
You can think of adding radicals like adding 4x + 6x which is 10x.
You have 4 x's and 6 more x's, so you have 10 x's all totaled.
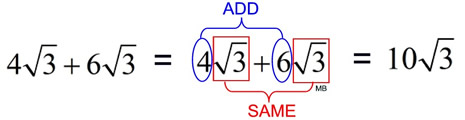
When radicals are the SAME, add the numbers right tight in front of the radicals.
Think: there are 4 square roots of 3 plus 6 square roots of 3.
That makes 10 square roots of 3 in total.
It may be necessary to simplify first!
Different looking radicals may actually be the same when simplified.
 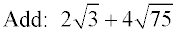
At first glance, it appears that combining these terms under addition is not possible since the radicals are not the same. But if we look further, we can simplify the second term so it will be a "like" radical:
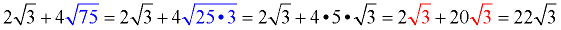
ANSWER: 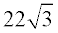
|
Some radicals cannot be added!
 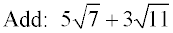
The radicals are different and each is already in simplest form. There is simply no way to combine these values. The answer is the same as the original problem.
ANSWER: 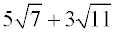 |
Remember, there may be an unwritten ONE in front of a radical!
 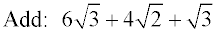
There is an implied "1" in front of 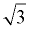 . All radicals are already in simplest form. Combine the "like" radicals. . All radicals are already in simplest form. Combine the "like" radicals.
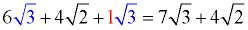
ANSWER: 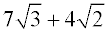 |
 REMEMBER: Always simplify first! When the radicals in an addition or subtraction problem are different, be sure to check to see if the radicals can be simplified. It may be the case that when the radicals are simplified, they will become "like" radicals, making it possible for them to be added or subtracted. REMEMBER: Always simplify first! When the radicals in an addition or subtraction problem are different, be sure to check to see if the radicals can be simplified. It may be the case that when the radicals are simplified, they will become "like" radicals, making it possible for them to be added or subtracted. |