"Simplifying" does not mean approximating.
"Simplifying" does not mean using your calculator to obtain a decimal estimate.
Simplify means to find another expression with the same value. |
We have seen radical values which can be simplified: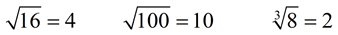
Are there other radical values which can be written in a simpler form?
Yes. There are square root values and cube root values which can be written in an equivalent form which is easier to understand (simplified). The process will depend upon the use of perfect squares and perfect cubes.
 Simplifying Square Root Values: |
 |
|
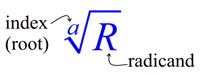A square root is in simplest form when
1.
the radicand contains no perfect square factors
2. the radicand is not a fraction
3. there are no radicals in the denominator of a fraction. |
 
1. Find the largest perfect square
factor (the largest perfect square that divides into 48 with no remainder). You need to be familiar with the list of perfect squares.
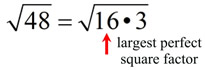
2. Give each factor its own radical symbol.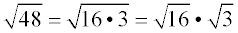 
3. Reduce the "perfect square" radical that was created.
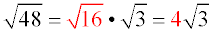
4. ANSWER: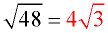 
Don't worry if you do not pick the LARGEST perfect square factor to start. You can still get the correct answer, but you will have to repeat the process. See what happens if we choose 4 instead of 16 to start:
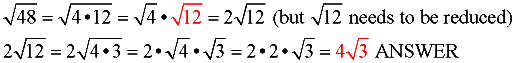
Notice how the out-front 2 in the second line is multiplied along for the rest of the problem.
|
 
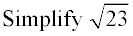
The number 23 cannot be factored by any of the perfect squares (23 is prime). This is a trick question as it is already in simplest form and cannot be reduced further.
If the number under the radical cannot be divided evenly by any of the perfect squares, your radical is already in simplest form and cannot be reduced further.
 
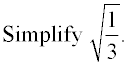1. Give the numerator and denominator their own radical symbols.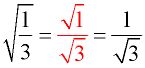 
2. Multiply the numerator and denominator by a radical that will get rid of the radical in the denominator, by creating a perfect square under the radical. If a smaller value cannot be found, multiply by the same radical value that is in the denominator, automatically creating a perfect square.
 
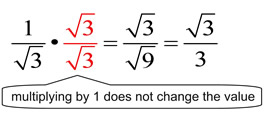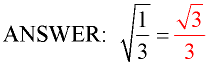
This process of removing a radical from the denominator is referred to as "rationalizing the denominator" because it turns the denominator into a rational (not irrational) value.
 
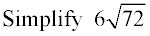
Let's see how this approach works with Cube Roots:
 
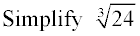
1. Find the largest perfect cube
factor(the largest perfect cube that divides into 24 with no remainder).
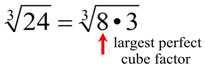
2. Give each factor its own radical symbol.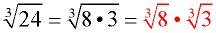 
3. Reduce the "perfect cube" radical that was created.
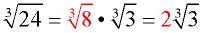
4. ANSWER: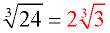 
|
