 Square of a Number
Finding the Square of a Number:
• Squaring a number is multiplying a number times itself.
| |
square of 7 = 7 x 7 = 72 = 49
square of n = n x n = n2 |
• Perfect squares are the squares of integers. (Examples shown at the right.)
You may also find definitions that state a perfect square is the square of any rational number. |
| |
Squaring a number creates a power (exponent) of 2 (or an even power). |
|
When numbers are "squared", even powers (exponents) are created.
 |
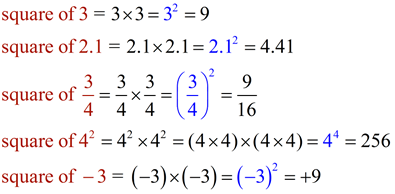Notice:
square of 3 = +9
square of -3 = +9
Same result ! |
|
Square Roots:
Square roots have an index value of two. When you see a radical with no index listed, it is assumed to be an index of two, a square root.
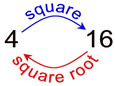
Finding the square root of a number is the inverse operation of squaring the number.
4 squared = 16
square root of 16 = 4 |
 |
Finding the Square Root of a Number:
• Square root of a number, n, is the number that gives n when multiplied times itself.
Now, you might ask, "can't the answer also be -5, since -5 x -5 = 25?"
• When no sign is indicated in front of 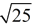 , it is referred to as the "principal square root" and the only answer is the positive answer.
• If the negative answer is expected, you will see  .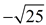
• If both positive and negative answers are expected, you will see  .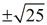
For example, when solving the equation x2 = 25, you are searching for both solutions: +5 and -5. So, we write: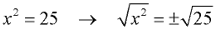 
• Examples of square roots of perfect squares are shown at the right.
• The value 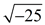 is not a real number and is not studied at this level.
|
Note: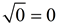 
Cube of a Number
Finding the Cube of a Number:
• Cubing a number is multiplying a number times itself three times.
| |
cube of 7 = 7 x 7 x 7 = 73 = 343
cube of n = n x n x n = n3 |
• Perfect cubes are the cubes of integers. (Examples shown at the right.)
|
| |
Cubing a number creates a power (exponent) of 3 (or multiple of 3). |
|
When numbers are "cubed", powers that are multiples of 3 are created.
 |
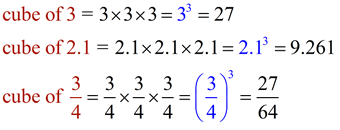Notice:
cube of 3 = +27
cube of -3 = -27
NOT the same ! |
|
 |
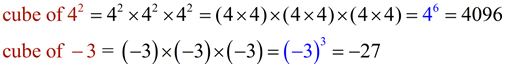Cube Roots:
Cube roots have an index value of three.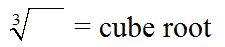 
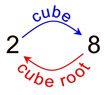
Finding the cube root of a number is the inverse operation of cubing the number.
2 cubed = 8
cube root of 8 = 2 |
 |
Finding the Cube Root of a Number:
• Cube root of a number, n, is the number that gives n when multiplied times itself three times.
When square rooting, we saw that the result may be both positive and negative. That is NOT the case when cube rooting. -2 x -2 x -2 = -8 ≠ +8
• Examples of cube roots of perfect cubes are shown at the right.
|
 When working with cube roots, it is easy to forget to write the index value of 3 on the symbol. Be careful! Without the 3 written in the cube root symbol, your answer will be incorrect, as it represents a different value.
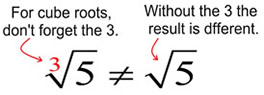
The cube root of 5 does not equal the square root of 5.
|
Perfect Squares
0 = 0 x 0
1 = 1 x 1
4 = 2 x 2
9 = 3 x 3
16 = 4 x 4
25 = 5 x 5
36 = 6 x 6
49 = 7 x 7
64 = 8 x 8
81 = 9 x 9
100 = 10 x 10
121 = 11 x 11
144 = 12 x 12
169 = 13 x 13
196 = 14 x 14
225 = 15 x 15 |
Grade 8 - NGMS
needs to know perfects squares up to 225.
Perfect Cubes
8 = 2 x 2 x 2
27 = 3 x 3 x 3
64 = 4 x 4 x 4
125 = 5 x 5 x 5
216 = 6 x 6 x 6
343 = 7 x 7 x 7
512 = 8 x 8 x 8
729 = 9 x 9 x 9
|
Grade 8 - NGMS
Needs to know perfect cubes up to 125.
|
|
Radicals on the Number Line
Three situations for graphing radical values on a number line:
1) The square root of a perfect square integer will be an integer whose exact value is easy to plot.
(An integer which is a rational number.)
2) The cube root of a perfect cube integer will be an integer whose exact value is easy to plot. (An integer which is a rational number.)
3) If you are not dealing with option 1 or 2, you will need to estimate the value of the square root or cube root before plotting. These plots will be "estimates" or "approximations" of the actual values.
(Irrational numbers.)
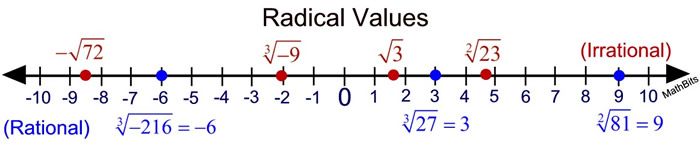
The rational numbers are plotted as exact values.
The irrational values are plotted as approximations.
The square root of a non-perfect square is an irrational number.
|
