Square roots and cube roots are put to work when solving certain types of equations.

Square root and cube root symbols are used to represent solutions to equations
of the form x2 = p and x3 = p, where p is a positive rational number.

Example 1:
Solve the equation x2 = 36.
Solution:
This question is asking "what number, or numbers, when squared will yield 36?"
By observation, we can determine that BOTH +6 and -6, when squared, will yield 36.
When solving this equation, we write:
eq1a

We need to solve for x.
To un-do x2, take the square root of both sides of the equation.
Write ± in front of the square root as two answers are possible.
Since 36 is a perfect square, we write the answer as ±6.
Both 6 x 6 = 36 and -6 x -6 = 36

The symbol ± indicates that BOTH the positive and negative solutions to the square root are being sought.

dividerdash

Example 2:
Solve the equation x2 = 27.
Solution:
Since 27 is not a perfect square, the solution to this problem will not be a nice integer value. Since this problem does not specify how the answer is to be expressed, we may state the answer as a un-simplified square root, a simplified square root, or as an approximation.
Not-simplified solution:
e1
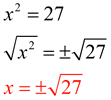Simplified solution:
e2
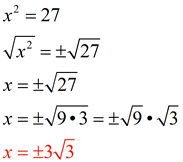Solution with approximation:
e3
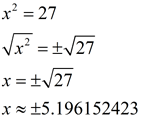If this question had asked for an "exact" answer, the only correct solutions would be either the not-simplified solution or the simplified solution. The approximation would not be considered correct as it is an "estimate" and not an "exact" answer.

dividerdash

Example 3:
Find the length of the hypotenuse of a right triangle whose legs measure 5 inches and 12 inches.
Solution:
Pythagorean Theorem: c2 = a2 + b2
Let a = 5, b = 12 and c = x.
x2 = 52 + 122
x2 = 25 + 144
x2 = 169
py
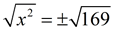
169 is a perfect square (13 x 13)
x = ±13 , but only +13 is the answer in this problem.
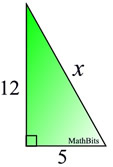 greentri
Remember, length cannot be negative,
(you cannot measure a negative length)
so in this problem the ONLY answer is +13 inches.

dividerdash

Example 4:
Find the length of the hypotenuse of a right triangle whose legs measure 6 inches and 9 inches.
Solution:
Pythagorean Theorem: c2 = a2 + b2
Let a = 6, b = 9 and c = x.
x2 = 62 + 92
x2 = 36 + 81
x2 = 117
eq5
117 is a NOT perfect square
x ≈±10.81665383, but length cannot be negative,
so the answer is just the positive answer.

redtru

A simplified radical answer is
rr

The simplified radical answer, or just simply rad17, is referred to as the "exact" answer.

dividerdash

Example 5:
Find the side of a cube whose volume is 27 cubic inches.
Solution:
Volume of cube: V = side3
Let side = x.
V = x3
27= x3
x3 = 27
v1
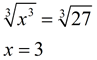
x = 3 inches

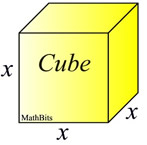
yelcube

A cube has length, width and height of the same measure.

The volume of a rectangular solid is V = l•w•h,
or in this case V = x3,
since l = w = h = x.

 
divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".
a