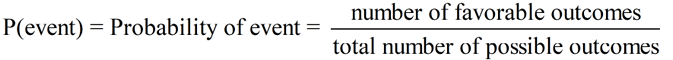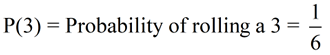|
|
Probability is how likely something is to happen.
|
When attempting to predict "how likely" an event is to happen,
or the "chance" that an event will occur,
numbers, in the form of ratios, are used.
Such a ratio is called the probability.
Outcomes are the possible results of an action (such as tossing a coin).
To find the probability ratio of such an action, we need to know
how many possible results (outcomes) are actually possible,
and how many of those results are what we are hoping will occur (favorable outcomes).
For example, when tossing a penny, you can get either
a "head" or a "tail".
The probability of getting "heads" on the toss of a penny
is the ratio 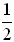 .
"Heads" is one of two possible outcomes when a penny is tossed, and the favorable outcome, in this case, is getting "heads". |
|
Probability can be expressed as: the ratio of the number of times it can occur (favorable outcomes)
to the total number of outcomes possible.
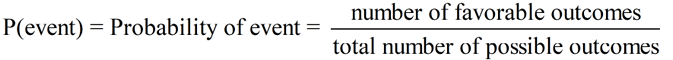
An event is a collection (subset) of possible outcomes.
A simple event is an event with a single outcome.
A compound event is an event that is the joining together (union) of two or more simple events.
Example: What is the probability of rolling a 3 on a fair die?
There are six possible results when a die is rolled:
{1, 2, 3, 4, 5, 6}
Total number of possible outcomes: 6
Number of favorable outcomes: 1 (the number 3)
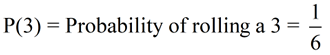
|
|
NOTE: The probability of an event found in this manner is referred to as theoretical probability,
because "in theory" the chance that an event will occur is based upon the number of times the event is possible, in relation to the total number of possible outcomes.

Ratios are most often expressed in the form of a fraction. Fractions, however, can also be expressed as decimals or percents. So probabilities may be expressed as fractions, decimals or percents.
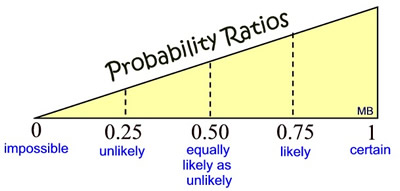
Probabilities range from 0 to 1. |
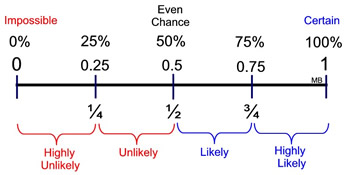
Probability as percents, decimals, fractions:
|
One or more outcomes are referred to as events.
If an event is impossible and will never occur, the probability is 0.
If an event is absolutely certain to occur, the probability is 1.
If an event is as equally likely, as unlikely, to occur, the probability is 0.5.
Otherwise, the value of a probability is between 0 and 1.

Events that are likely to occur have a probability greater than 0.50.
(values between 0.75 and 1 are usually referred to as highly likely to occur)
The closer a probability gets to 1, the more likely the event will occur.
Events that are unlikely to occur have a probability less than 0.50.
(values between 0 and 0.25 are usually referred to as highly unlikely to occur)
The closer a probability gets to 0, the less likely the event will occur.
|
Note: The "vocabulary" for describing "likelihood" may vary slightly between textbooks (such as "certain not to happen" instead of "impossible"). These differences should not cause a problem in understanding the meanings of the expressions.
 |
Remember: Probability can never be greater than one,
or less than zero.
Probability ratios have a numerator
(top) that is less than or equal to
its denominator (bottom).
(Note: neither the top nor the bottom can be a negative number.)
|
|
Note: When working with probability, fractions may be left in unreduced form unless the directions indicate that reducing the fractions is required. You may, however, see reduced fractions as answers in multiple choice questions.

While probability was originally developed to deal with gaming techniques, it is used today in a wide range of applications. Even common sayings reflect the concept of probability.
Someone says "Don't hold your breath" when you are waiting for something to happen. What is the person implying about the probability that the event will occur in the near future? |
 |
ANSWER: This statement implies that you may die holding your breath waiting for this event to occur.
Obviously, the probability of the event occurring in the near future, is extremely low, if not impossible.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|