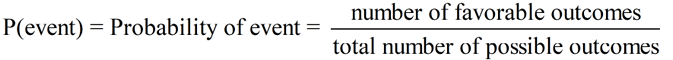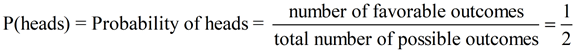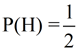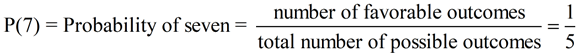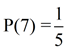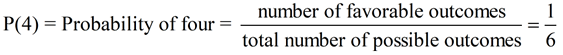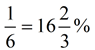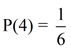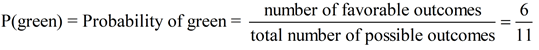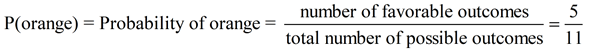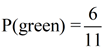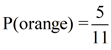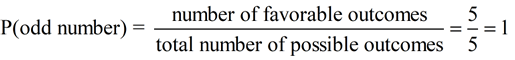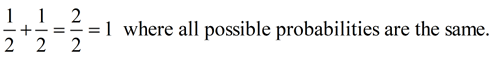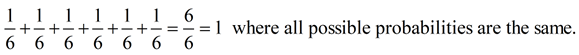|
Basic probability deals with simple events.
Simple events (or single events) are events with a single outcome.
 |
In plain English, a simple event deals with one "thing" (event) happening - tossing one penny, rolling one die, picking one card, spinning one spinner, drawing one marble, etc. As opposed to tossing 3 pennies, rolling two dice, picking two cards, spinning one spinner AND rolling one die, tossing a penny AND drawing a card, etc, which are compound events..
|
|
|
Probability is the chance that an event will occur. It is measured by the ratio of the favorable outcomes to the total number of outcomes possible. |
|
Let's see how we can apply this ratio formula:

Tossing a fair coin: If a penny is tossed into the air, it is going to land showing either heads up, or tails up. There are only two possible outcomes when a penny is tossed (a head or a tail). Since this is a fair coin, the probability of either outcome is equally likely. What is the probability of tossing heads?
Total number of outcomes possible = 2 (heads or tails)
Number of favorable outcomes = 1 (heads)
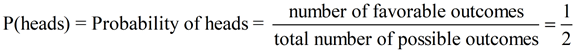
The probability of getting heads on the toss is the ratio 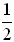 , or 50%. , or 50%.
|

Probability of heads
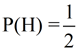
equally likely as
unlikely to occur
|
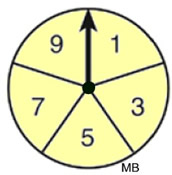
Using a Spinner: The spinner in this example is divided equally into five sections, numbered {1, 3, 5, 7, 9}. Upon spinning, the arrow has an equally likely chance of landing on any of the five sections.
What is the probability of landing on 7?
Total number of outcomes possible = 5 ({1, 3, 5, 7, 9})
Number of favorable outcomes = 1 (landing on
7)
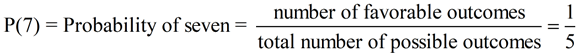
The probability of getting "7" on a spin is the ratio 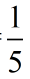 , or 20%. , or 20%.
|
Probability of "7"
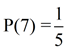 not likely to occur
not likely to occur
|
Rolling a fair die: A fair die is rolled. A die is a 6-sided cube where each side is uniquely numbered 1 through 6 with dots. Outcomes = {1, 2, 3, 4, 5, 6}. Since this is a fair die, there is an equally likelihood of rolling any of the 6 possible outcomes. What is the probability of rolling a 4?
Total number of outcomes possible = 6 ({1, 2, 3, 4, 5, 6})
Number of favorable outcomes = 1 (rolling a 4)
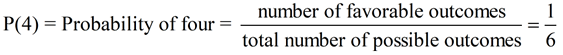
The probability of getting "6" on a roll is the ratio 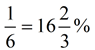 . .
|
 Probability of "4"
Probability of "4"
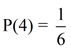 not likely to occur
not likely to occur
|
 |
NOTE: When rolling a "fair" die, the probability of rolling a number 1, 2, 3, 4, 5 or 6
has the same chance of happening. Each value is "equally likely to occur".
When probability is equally likely to occur, the situation is described as being "fair".
There are oddly shaped, or weighted, die where the faces are not equally likely to occur when tossed.
|
|
When the probabilities of the outcomes are equally likely to occur, as seen in the three examples above, the situations are referred to as uniform probability models. |
 Now, we will examine some non-uniform probability models.
Let's see what happens if the favorable outcome (ratio top) is more than 1. |
In a non-uniform probability model, there is more than one way to secure a favorable outcome, That is, there will be more than one of the possible outcomes that will satisfy what we are looking for.
Pulling beans from a jar: Consider the situation of drawing a bean from a jar containing
6 green beans and 5 orange beans.
Since there are more green beans than orange beans,
there will be a greater possibility of drawing a green bean.
When drawing a bean, the color choices are not equally likely to occur.
What is the probability of drawing a green bean?
There are 6 ways to draw a green bean.
Total number of outcomes possible = 11 (11 beans in the jar)
Number of favorable outcomes = 6 (6 ways to get a green bean)
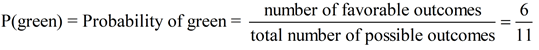
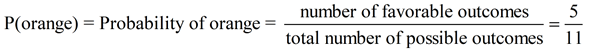
|
Probability of "green"
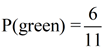 Probability of "orange"
Probability of "orange" 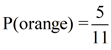
|


Let's revisit that spinner: The spinner in this example is divided equally into five sections, numbered {1, 3, 5, 7, 9}. Upon spinning, the arrow has an equally likely chance of landing on any of the five sections.
What is the probability of landing on an odd number?
Total number of outcomes possible = 5 ({1, 3, 5, 7, 9})
Number of favorable outcomes = 5 (they are all odd numbers)
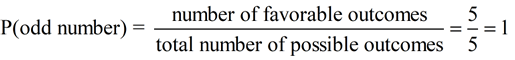
The probability of getting "an odd number" on a spin is 1, or100%.
|

Probability of "odd"
P(odd) = 1
certain to occur |

Let's revisit rolling a die:
We know there are 6 possible outcomes: {1, 2, 3, 4, 5, 6}
Now, however, we will encounter a variety of possible favorable outcomes.
|
State the probability of each of the following favorable outcomes, along with a description of its likelihood: certain to happen, certain not to happen, likely to happen, likely not to happen.
You may assume that this is a fair die.

Possible rolls:
1, 2, 3, 4, 5, 6
|
• rolling a 2 |
• probability = 1/6 likely not to happen |
• rolling a number less than 3 (1, 2) |
• probability = 2/6 likely not to happen |
• rolling a 7 |
• probability = 0 certain not to happen |
• rolling a number less than 10 |
• probability = 1 certain to happen |
• rolling a number greater than 1 |
• probability = 5/6 likely to happen |
• rolling a factor of 6 (1, 2, 3, 6) |
• probability = 4/6 likely to happen |
• rolling a number that is an integer |
• probability = 1 certain to happen |
• rolling a negative number |
• probability = 0 certain not to happen |
Note: The "vocabulary" for describing "likelihood" in this example was slightly different (such as "certain not to happen" instead of "impossible"). Different textbooks may use slightly different expressions, so you need to be flexible and adjust when needed.


What is occurring with the sums of the probabilities of possible outcomes for the examples on this page?
• Coin Toss: (uniform probability)
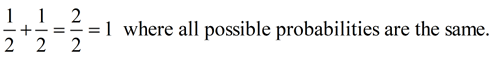
• Using a Spinner: (uniform probability)

• Rolling a Die: (uniform probability)
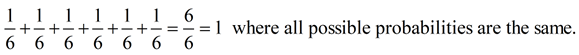
• Pulling a bean: (non-uniform probability)

 Conclusion: When all possible probabilities (for all outcomes) are added, the result will be "1" (which is the same as 100%). This remains true whether the probabilities are all equal to one another, or not. Conclusion: When all possible probabilities (for all outcomes) are added, the result will be "1" (which is the same as 100%). This remains true whether the probabilities are all equal to one another, or not.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|