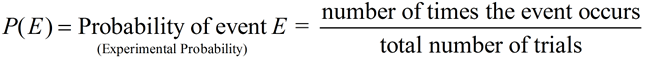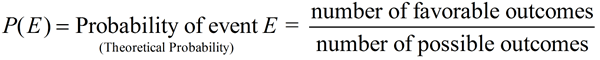We have seen references to the term "theoretical probability" in previous lessons.
Theoretical probability is the probability that is the ratio of favorable outcomes
to the total possible outcomes. It is the probability that, in theory, is expected to occur.

We are now going to investigate "experimental probability"
which is the probability that is observed during an experiment.

Experimental Probability



When you gather data from observations during an experiment, you will be calculating an experimental probability.

The experimental (or empirical) probability of an event is an "estimate" that an event will occur based upon how often the event occurred after collecting data from an experiment in a large number of trials. This type of probability is based upon direct observations. Each observation in an experiment is called a trial.
 rollpiclabel
peex

dividerdash

Example:
A survey was conducted to determine students' favorite brands of sneakers.
Each student chose only one brand from the list of brands A, B, C, D, or E.
What is the probability that a student's favorite sneaker was brand D?
Sneaker
A
B
C
D
E
Number
12
15
24
26
13

 

 


Answer: There were 12 + 15 + 24 + 26 + 13 = 90 "trials" in this experiment (each student's response was a trial).

26 out of the 90 students chose brand D.
The probability is :
     probans

 
According to this experiment, the probability is 13/45. Another experiment with a different group of students will most likely give a different probability of the popularity of Brand D sneakers.
The value 13/45 is called the experimental probability.

dividerdash


Theoretical Probability



With theoretical probability, you do not actually conduct an experiment. Instead, you use what you know about the situation to determine the probability of an event occurring. You may use your reasoning skills or an existing formula to arrive at your answer.

The theoretical probability of an event occurring is an "expected" probability based upon knowledge of the situation. It is the number of favorable outcomes to the number of possible outcomes.
expectprob
theoprob

dividerdash

Example:
Find the probability of rolling a 6
on a fair die.

reddie

 

 


Answer: No experiment is needed. There are 6 possible outcomes when rolling a die: 1, 2, 3, 4, 5, and 6.
The only favorable outcome is rolling a 6.

The probability is :
    theoans

Under the best circumstances, we would expect to roll one 6 out of every 6 rolls.

dividerdash


Comparing Experimental and Theoretical Probabilities

 
In an experiment, two dice are rolled 50 times and the sum of the faces are recorded in a chart, as shown at the right.
1) What is the experimental probability of rolling an 8?

2) What is the theoretical probability of rolling an 8?

3) How do the experimental and theoretical probabilities compare?
Experiment Results:
Sum of Rolls of Two Dice
4,6,4,8,10,8,6,11,9,2
3,6,12,5,6,8,4,8,7,11
5,2,8,3,9,4,10,3,5,3
7,8,3,11,6,4,8,3,6,4
11,9,7,8,5,9,3,6,7,4,
Solution:
1) Experimental probability is the probability observed during an experiment of rolling two dice. The results are in the chart above. The 8 was rolled 8 times out of 50 rolls. The experimental probability = 8/50 = 16%
.
2) Theoretical probability is based upon what is expected when rolling two dice, as seen in the "sum" table at the right.
This table shows all of the possible sums when two dice are rolled. The theoretical probability of rolling an 8 is 5 times out of 36 rolls. The theoretical probability = 5/36 ≈ 13.9%.

3) The experiment rolled more 8's than would be expected theoretically. Theoretically, you would expect to roll a sum of 8 approximately 6.9 times out of 50 rolls.
5/36 = x/50 and x ≈ 6.9 times
Theoretical Results:table


smallstar Experimental probability approaches theoretical probability
when the number of trials is extremely large.

The Law of Large Numbers (called Bernoulli's Theorem) states:
"If an experiment is repeated a large number of times, the experimental probability of a particular outcome
approaches a fixed number as the number of repetitions increases. This fixed number is the theoretical probability.


divider


NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".