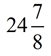On this page we are going to look at examples of random selection using a random number table.

Each home-room teacher is to select 3 students to send to a Student Council assembly. Mr. Stevens has 15 students in his home-room and he wants to choose the 3 students at random, using a random number table.
Solution Method 1: Mr. Stevens knows that he will need to pick 2-digit numbers (01 - 15) from the Random Number Table to represent his students. A random number table can be used to read 2-digit numbers, but the range will be 00 to 99. This means that Mr. Stevens may have to look through a large group of numbers before finding three numbers between 1 and 15.
Mr. Stevens chooses to start in the upper left corner of the table (he could have started at any point in the table) and begins dividing every 2-digits horizontally until he has found three 2-digit numbers between 01 and 15 to represent the chosen students.

Random Number Students 11, 15, and 13 will be sent to represent the home-room.
Solution Method 2:
 |
Mr. Stevens decided that he did not like the method in Solution 1 because he thought it was tedious trying to keep track of the divisions for 2-digit numbers and it felt time consuming.
Since he is only interested in number 01 to 15, he decides to shorten his search in the Random Number Table by assigning sets of 6 numbers to each of the students. In this way, he will only need to pick the first three two digit numbers (or a couple more if he hits a "skipped" number) from the table for the chosen students.
Mr. Stevens divided 100 possible 2-digit numbers in the chart by 15 students and found out that he could assign 6 two digit numbers to each student. See chart at the left.
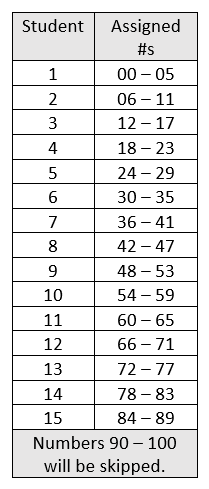
He now chooses the first three 2-digit numbers from the chart:
36, 51, and 83 which will be students 7, 9, and 14 respectively.
|
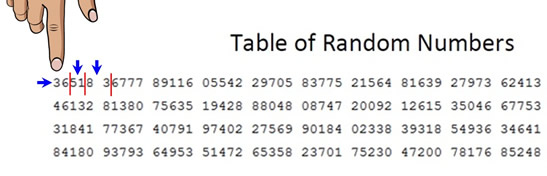
Solution Method 3: Mr. Stevens also has another option for choosing students from the Random Number Table. He can pick the first two digits from each 5-digit grouping in the table, either horizontally or vertically. The table below shows moving horizontally. It may be visually easier to find the numbers this way than having to keep dividing up the numbers into sets of 2. Students 5, 8, and 12 were chosen.



Jake's younger sister is collecting the figurines that come in child-size "Fun Meal" boxes from a fast-food restaurant. There are a total of 5 different figurines. Jake wants to know how many "Fun Meal" boxes, on average, would have to be purchased for a child to collect all 5 figurines?
Solution: Jake is using a Random Number Table to simulate buying boxes of "Fun Meals" where the numbers 1 through 5 represent boxes with the 5 different figurines. Each digit represents purchasing one "Fun Meal". If the digit is 1, 2, 3, 4, or 5, the "Fun Meal" contains that specific figurine. Jake keeps reading across the table until he has found the digits 1 through 5. The number of digits that he has to look at before arriving at all five numbers, represents the number of boxes that had to be bought before all 5 figurines were found.
A section from the Random Number Table Jake used is shown below. The black arrows show the starting point for each of his eight trials. One grouping of numbers in the chart was "skipped over" between each trial only for the purpose of labeling and ease of reading.