At this level, the events that we will be dealing with will be independent.
One event will not have an affect on the other event.
You have already seen questions that contain statements such as
"returned to the bag" or "returned to the deck". These are important statements.
On this page we are only going to take a quick look at why this is an important concern,
as this knowledge will be used in future mathematics courses.
When working with compound events,
it is important to know if the first event affects the second event.
For example:
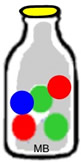
What is the probability of drawing a red marble,
then drawing a blue marble from this jar?
The probability of drawing a red marble = 2/5.
The probability of drawing a blue marble = 1/5.
BUT...
|
|
• The 1/5 probability of drawing a blue marble assumes all 5 marbles are in the jar.
•
What happens if you draw the first marble and do NOT put that marble back in the jar before drawing the second marble? If the marble is not "replaced", the probability of the second drawing changes, since there are less marbles in the jar.
The probability of drawing a red marble = 2/5.
 Without putting the marble back in the jar, Without putting the marble back in the jar,
the probability of drawing a blue marble is now = 1/4.
Let's compare the two different final answers:
| With Replacement: |
Without Replacement: |
 |
The probability of drawing a red marble = 2/5.
Put the marble back in the jar.
The probability of drawing a blue marble = 1/5. (of the 5 in the jar)
Answer: 2/5 • 1/5 = 2/25 |
|
 |
The probability of drawing a red marble = 2/5.
Do NOT put marble back in jar.
The probability of drawing a blue marble = 1/4. (of the 4 left in jar)
Answer: 2/5 • 1/4 = 2/20 = 1/10 |
|
|
|
Compound events where the first event DOES affect the second event are called dependent events.
Dependent events especially show up when you are physically "picking" things up, or moving things, - like picking cards. picking marbles, or picking numbered/colored chips. When you "pick it up", and do not put it back, you change the sample space for the next event.



