|
Developing a model means that we are going to conduct our own experiment and record our "experimental" probabilities.
A probability model is an organized way of showing all of the possible outcomes and their experimental probabilities. Models on this page will be designed using a table.


Develop a model to investigate rolling a specific number on a fair die.
(we will be testing to see if our experimental results will be the same as the theoretical probability).
Testing for Rolling a 2: The theoretical probability of rolling a 2 on a fair die is 1/6 (or 16.7%). This result has a single outcome, so this is called a simple event.
Experiment:
a) Collect the data: roll a die 40 times and record the results
b) According to the data, the experimental probability of rolling a 2 is:
5/40 = 1/8 (or 12.5%)
This is not the expected result. It could be argued that, in this case, the difference is due to the fact that the die rolling was done using an on-line simulator, which is run by an algorithm and is not truly random.
c) Compare predictions made using the experimental findings with predictions made from the theoretical probability ratios for rolling a die: |
 Rolling a Two
Rolling a Two
Die # |
Frequency |
1 |
12 |
2 |
5 |
3 |
7 |
4 |
9 |
5 |
4 |
6 |
3 |
|
•
If 200 rolls of the die occurred, what would be the frequency of rolling a 2,
predicted by the experimental findings? 1/8 of 200 = 1/8 x 200 = 25 times
• What would be the frequency of rolling a 2, predicted by the theoretical probability ratios
for rolling a die? 1/6 of 200 = 1/6 x 200 = 33.3 times
|


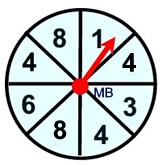
Develop a model to investigate a spinner arrow landing on a specific value.
(look carefully at this spinner)
Testing for Landing on a 1: While the sections on this spinner are of equal size (or area), the sections' numberings are not unique. While there are 8 sections on the spinner, there are 3 sections numbered "4" and 2 sections numbered "8", This is NOT a uniform probability model where each possible outcome is equally likely to occur.
Theoretical probability of 1, 3, or 6 is 1/8 for each.
Theoretical probability of 4 is 3/8.
Theoretical probability of 8 is 2/8.
a) Collect the data: spin the arrow 40 times and record the results.
b) According to the data, the relative frequency (experimental probability) of landing on a 1 is 4/40 = 1/10
This is not an exact match for the theoretical probability, but it is close. |
 Landing on 1
Landing on 1
Spin
# |
Frequency |
1 |
4 |
3 |
2 |
4 |
14 |
6 |
9 |
8 |
11 |
|
c) Comparing predictions made using the students' experimental findings, or relative frequency, with predictions made from the theoretical probability ratios for a spinner landing on a specific value.
•
If 600 spins occur, what would be the frequency of landing on a 1, predicted by the
students' findings? 1/10 of 600 = 60 times
• What would be the frequency of the spinner landing on a 1, predicted by the theoretical
probability ratios for landing on 1? 1/8 of 600 = 1/8 x 600 = 75 times
|
Will the rest of the results in the chart also show this "close" result
when comparing the other experimental and theoretical predictions? |
Let's see what happens with predicting results for all of the values from the table on 600 spins:
Predications for Each Spin Number after 600 Spins
Spin # |
Frequency
out of 40
|
Experimental
Prediction |
Theoretical
Prediction |
Prediction
Difference |
1 |
4 |
60 |
75 |
+15 |
3 |
2 |
30 |
75 |
+45 |
4 |
14 |
210 |
225 |
+15 |
6 |
9 |
135 |
75 |
-65 |
8 |
11 |
165 |
150 |
-15 |
While the prediction comparison between the experimental prediction and the theoretical prediction of spinning a "1" did not seem too far apart, predictions on some of the other spin numbers show more drastic differences. This shows us that while one of the results from an experimental table may create predictions close to the theoretical predictions, we should not assume that the other results in the table will do the same.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|



