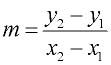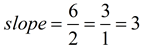|
 Things you need to know to work with equations of lines: Things you need to know to work with equations of lines:
Slope formula based on coordinates:
(Slope is represented by "m")
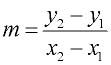 The change in y, over the change in x.
The change in y, over the change in x.
Rise / Run
|
The slope of a straight line is constant
(it does not change).
|
Points on Lines:
If a point lies on a line, the coordinates of the point (x, y) make the equation true.
• Does (4,7) lie on the line y = 3x - 5?
Yes. using x = 4 and y = 7, we have
7 = 3(4) - 5
7 = 12 - 5
7 = 7 True. |
If you need to refresh your knowledge on "slope",
see Slope and Rate of Change.
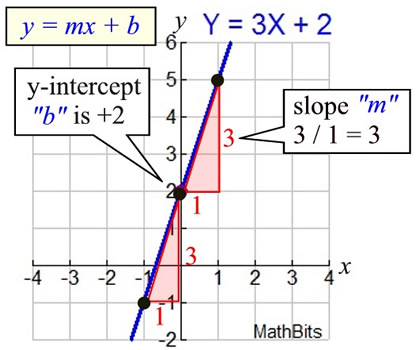
 Equation of a Straight Line: y = mx + b
m = slope; b = y-intercept
|
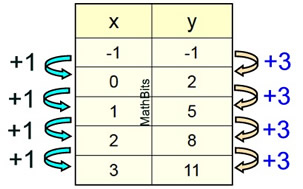
The line at the right passes through
points (-1,-1), (0,2), (1,5)
(all of these (x,y) values make the equation
y = 3x + 2
true)
"m" = slope
The slope is the rate of change
occurring along the line.
The triangles show the rate of change in the x-values (1) and the y-values (3) between the points.
The slope of this line is 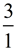 = 3. = 3. |
|
If we check the slope using (-1,-1) and (1,5), there will be an x-value change of 2 and a y-value change of 6.
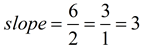
"b" = y-intercept
(where the line crosses the y-axis)
|
Slope of 3: For every change of 1 on the x axis,
there will be a change of 3 on the y-axis.
Slope = 3 / 1 = 3 |
y = mx + b is called the Slope-Intercept Form of a straight line.
(m = slope; b = y-intercept)
|
|
When using this form,
you can only read the slope and y-intercept when the equation starts with "y =" .
No numbers (or letters) in front of the "y".
If the equation does not start with "y=", you will need to rewrite the equation so it does start with "y=" before reading the slope and/or y-intercept. |

 Find the slope and y-intercept of the equation y = 4x - 1. Find the slope and y-intercept of the equation y = 4x - 1.
Solution: This is an easy one! This equation is already in the "y = mx + b" form. The m = 4 and the b = -1.
Remember that y = 4x - 1 is the same as y = 4x + (-1), so the b = -1.
Slope (m) is 4 and y-intercept (b) is -1
 Find the slope and y-intercept of the equation 2y = 6x + 4. Find the slope and y-intercept of the equation 2y = 6x + 4.
Solution:  There is a number in front of y. We need " y = mx + b" where the number in front of y is 1, before we can read off the slope and y-intercept. Rewrite this equation.
Divide all terms by 2 and get y = 3 x + 2.
Slope (m) is 3 and y-intercept (b) is + 2
 Find the slope and y-intercept of the equation 4x + 2y = 6. Find the slope and y-intercept of the equation 4x + 2y = 6.
Solution:  There's a number in front of y and y is not alone on one side of the equal sign. There's a number in front of y and y is not alone on one side of the equal sign.
We need some major rewriting on this equation.
First, get the y term by itself on one side of the equal sign. Subtract "4x" from both sides: 2y = 6 - 4x
Divide all terms by 2: y = 3 - 2x
Rewrite the right hand side so the x term is first. Be careful with the signs: y = -2x + 3
Slope (m) is -2 and y-intercept (b) is +3
 Write the equation of a line with a slope of 5 and Write the equation of a line with a slope of 5 and
a y-intercept at (0,-6).
Solution: If the y-intercept is at the point (0.-6), then the line crosses the y-axis at -6.
So, the given information tells us that m = 5 and b = -6.
Place these values in the form y = mx + b.
Equation: y = 5x + (-6) or y = 5x - 6
 |
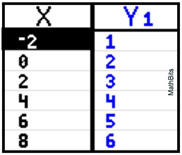
Write the equation of the line that produced this graphing calculator table. |
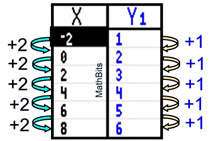 |
Solution: Examine the table.
The x-values are changing by +2 and the y-values are changing by +1. The slope, m, will be the change in y over the change in x, or ½.
The graph passes through the point (0,2), which is the y-intercept, so b = 2.
Use y = mx + b. Equation: y = ½x + 2 |
|
 |
 Write the equation of the line which passes through the Write the equation of the line which passes through the
points (-2,3) and (4, 6).
Solution: This problem can be tackled in several different ways.
•
You could plot the points and carefully draw the line so you could determine the slope and see the y-intercept. But that y-intercept could be tricky to find by observation.
• A better approach would be to find the slope by calculating the change in y over the change in x.
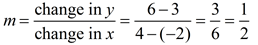 which let's you start creating an equation: y = ½x + b. which let's you start creating an equation: y = ½x + b.
To find the missing b, use one of the two points. If a point is "on" a line, it makes the equation of the line true.
Let's use (4,6) since positive values are easier. Remember (4,6) = (x,y). Plug into the equation for x and y.
y = ½x + b 6 = ½(4) + b 6 = 2 + b 4 = b.
Now, we have our equation: y = ½x + 4

There is another way to tackle Example 6.
It is a formula specifically designed for writing equations
when you are dealing with a point, or points, on the line.
 Equation of a Straight Line: y - y1 = m(x - x1)
m = slope; (x1, y1) = any point on the line |
y - y1 = m(x - x1) is called the Point - Slope Form of a straight line.
|
|
When you know a point on the line and the slope (or you can determine the slope), this form will save you some computation time.
Be sure to notice that you are subtracting x1 and y1.
|

 Find the equation of a line with a slope of -1 passing Find the equation of a line with a slope of -1 passing
through (-4,6).
Solution: The given information tells us that m = -1 and (x1, y1) = (-4,6)
Substitute into the form y - y1 = m(x - x1): y - 6 = -1(x - (-4))
Simplify: y - 6 = -1(x + 4) y - 6 = -x - 4 y = -x + 2
(Unless directed otherwise, write your equation in "y =" form.)
Equation: y = -x + 2
 Let's take another look at the previous Example 6. Let's take another look at the previous Example 6.
Write the equation of the line which passes through the
points (-2,3) and (4, 6).
Solution: First find the slope: 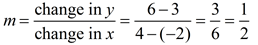
Choose either point. We will use (4,6). Those positive numbers are always friendlier.
Substitute into the form: y - y1 = m(x - x1): y - 6 = ½(x - 4)
Simplify: y - 6 = ½x - 2 y - 6 = ½x - 2 y = ½x + 4
Equation: y = ½x + 4

We have seen that lines can be positioned in four basic ways on a graph.
How do these positions affect the slope and the equation of the line?
 Slope is positive.
Slope is positive.
Lines that go "up hill".
The rise and run are
both positive.
y = mx + b
where m is positive.
|
 Slope is negative.
Slope is negative.
Lines that go "down hill".
The rise is negative
and run is positive.
y = mx + b
where m is negative. |
 Slope is zero.
Slope is zero.
Lines go "horizontal".
There is no rise (0)
and run is positive.
y = 0x + b = b
where m is zero. |
 Slope is undefined.
Slope is undefined.
Lines go "vertical".
There is no run (0).
Division by zero in
rise / run !!!!
x = x-intercept number |
We have been working with the first two situations, where m can be either positive or negative. Let's take a closer look at the last two odd ball situations.
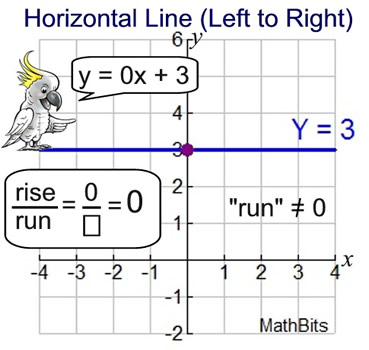
 Horizontal Lines: Horizontal Lines:
 Horizontal Line Equation: y = b Horizontal Line Equation: y = b
m = slope = 0; b = y-intercept
|
Horizontal lines are parallel to the x-axis.
• Horizontal lines have a slope of zero because they have lots of "run", but no "rise".
• The rise/run formula for slope always has a numerator of zero, making all of the ratios zero.
• The actual formula is y = 0x + b. Since 0x is not written, the equation becomes y = b.
• This equation describes what is happening to all of the y-coordinates of points that lie on the line (all y-coordinates are b). Points on the line have coordinates such as (-1,b), (0,b), (4,b), (10,b), and so on, where all of the y-coordinates are the same. |
 |
 Find the equation of a line passing through the points (1,4) and (6,4). Find the equation of a line passing through the points (1,4) and (6,4).
Solution: When you plot these points, you can see that the line will be horizontal.
The line will cross the y-axis at 4, making the y-intercept 4, so b = 4.
Equation: y = 4
 Find the slope of a horizontal line passing through (-4,-8). Find the slope of a horizontal line passing through (-4,-8).
Solution: All horizontal lines have a slope of zero.
The point (-4,-8) is not needed (it is a distraction).
Slope = 0.
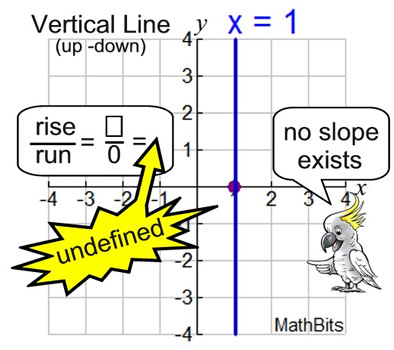
 Vertical Lines: Vertical Lines:
 Vertical Line Equation: x = "x-intercept value" Vertical Line Equation: x = "x-intercept value"
m = slope = undefined; b = y-intercept = not used
|
Vertical lines are parallel to the y-axis.
• Vertical lines have undefined slope (it does not exist) because they have lots of "rise", but no "run", creating a division by zero problem.
• The rise/run formula always has a denominator of zero, making all of the ratios undefined.
• The vertical line form is x = a number,
where the "number" is the x-intercept (where the line crosses the x-asix).
• Vertical line formulas never contain a y-value. |
 |
| • This equation describes what is happening to all of the x-coordinates of points that lie on the line (all x-coordinates are the x-intercept value). For example, if the x-intercept is 3, the points on the line have coordinates such as (3,-1), (3,0), (3,4), (3,10), and so on, where all of the x-coordinates are the same. (all x-coordinates are 3). |
|
When working with vertical lines, it is best to describe the slope as "undefined" (or "no slope exists") instead of saying only "no slope".
The expression "no slope" may be misinterpreted to mean a slope of 0.
Doesn't "no bananas" mean you have 0 bananas?
It does not mean that bananas do not exit. See the problem?
|
|
 Find the equation of a line passing through the points (7,4) and (7,-2). Find the equation of a line passing through the points (7,4) and (7,-2).
Solution: When you plot these points, you can see that the line will be vertical.
The line will cross the x-axis at 7.
Equation: x = 7
 Find the slope of a vertical line passing through (1,2). Find the slope of a vertical line passing through (1,2).
Solution: All vertical lines have no slope (or undefined slope). The slope does not exist.
The point (1,2) is not needed (it is a distraction).
Slope = undefined (does not exist).

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|