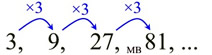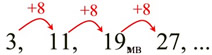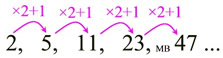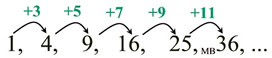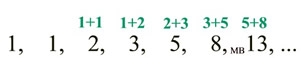"Seeing" Number Patterns: |
First, let's clarify that not all lists of numbers form a "pattern". It may likely be the case that there is no relationship between the numbers in a list.
But we will be looking at those lists of numbers where a relationship (a "pattern") does exist. Some of these number patterns will be easy to see, while others will be more difficult to decipher. |
|
List of Numbers |
Observations |
Pattern |
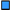 2, 4, 6, 8, 10, ... |
|
"2 is added to each
previous term in the list" |
 3, 9, 27, 81, ... |
|
"3 is multiplied times
each
previous term in the list" |
 3, 11, 19, 27, ... |
|
"8 is added to each
previous term in the list" |
In this next example, it would be harder to "see" the pattern. Adding a single number will not work.
Multiplying by a single number will not work. This pattern is a combination of multiplying and adding. |
 2, 5, 11, 23, 47, ... |
|
"multiply each previous
term times 2 and add 1" |
Connecting Patterns to Functions: |
When examining a list of numbers that form a pattern, it is often helpful to think about each term's position (location) in the list. For example, is a term the first number in the list? The third number in the list? Or the tenth number in the list? The number (location) of a term is always a natural number, {1, 2, 3, 4, 5, 6, 7, 8, ...}.
Let's take another look at this number pattern:  2, 4, 6, 8, 10, ... 2, 4, 6, 8, 10, ...
Number the terms: Assign a "counting" number to each of the terms in the number list. This will mark the location of each term in the pattern.

Remember the pattern:
 |
Create a table:
Place the location number and the
number list term in a table.
Location |
Number |
1 |
2 |
2 |
4 |
3 |
6 |
4 |
8 |
5 |
10 |
6 |
12 |
|
Using the location number as the x-coordinate, the number pattern can be graphed.
Each term's location is used to create a graph of the number pattern. The x-coordinate is the location number, and the y-coordinate is the number list term. The graph is a scatter plot. Do not connect the dots.
|
|
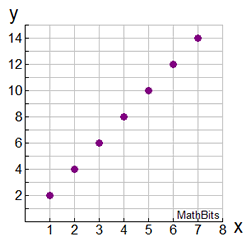 (x,y) = (location, term)
(x,y) = (location, term)
|
|
Create an equation for the pattern:
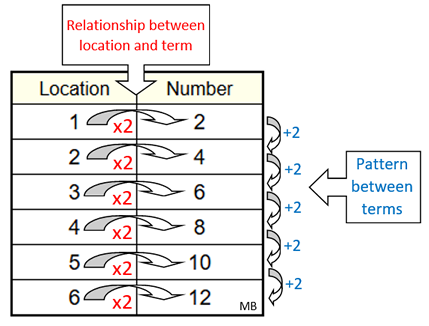 |
Because the pattern was +2 (addition of 2), between terms, we have:
Location |
Number |
1 |
2 |
2 |
4 = 2+2 |
3 |
6 = 2+2+2 |
4 |
8 = 2+2+2+2 |
5 |
10 = 2+2+2+2+2 |
6 |
12 = 2+2+2+2+2+2 |
where the location column is the number of 2's being added in the number column. |
You can see, from the tables above, that a relationship between the location number of a term and the term itself exists. Each term in the number list is twice its number location.
For example, the 3 in the location column means three 2's, which is 6, which is 2+2+2.
So, in this number pattern, we can use each term's location to create an equation: y = 2x
where x is the number location of the term and y is the term itself in the number list.
NOTE: Yes, y = 2x is normally graphed as a straight line, not as a scaatter plot of dots. But if we limit the x-values that we can use to just natural numbers {1, 2, 3, 4, 5, ...}, the equation y = 2x represents our dots.
An advantage of the "equation", when working with a number pattern, is that the 150th term can be found very quickly by plugging 150 into the equation. y = 2(150) = 300. The 150th term of this number pattern is 300.
|
FYI: Challenging Number Patterms: |
There are always patterns that stretch
one's investigative skills.
These patterns may seem obvious after seeing them,
but initially finding them may have seemed impossible.
Let's look at two of these more challenging sequences. |
 |
 1, 4, 9, 16, 25, 36, 49, ... 1, 4, 9, 16, 25, 36, 49, ... |
|
This is a more challenging pattern since the same number is not added each time. |
Solution one:
based on what is being added:
The numbers being added are the sequence of odd numbers.
Description: "each new term is found by adding the next odd number." |
Solution two:
based on each term's location
1 2 3 4 5 6 7
 1, 4, 9, 16, 25, 36, 49, ... 1, 4, 9, 16, 25, 36, 49, ...
Multiply each term's location
times
itself to get the number pattern
term.
Each term in this list is the
"square" of its number location. |
1 × 1 = 1
2 × 2 = 4
3 × 3 = 9
4 × 4 = 16
5 × 5 = 25
6 × 6 = 36
7 × 7 = 49 |
|
 1, 1, 2, 3, 5, 8, 13, 21, ... 1, 1, 2, 3, 5, 8, 13, 21, ... |
This famous number pattern is called:
The Fibonacci Sequence
|
The pattern:
Starting with the third term, add the previous two terms together.
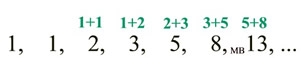
|
|