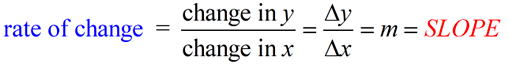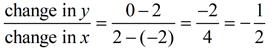|
 Linear Functions:
You are already familiar with the concept of "rate of change".
When working with straight lines (which are linear functions)
you discovered that "rate of change" was represented by the slope of the line.
The word "slope" may also be referred to as "gradient", "incline" or "pitch", and be expressed as:

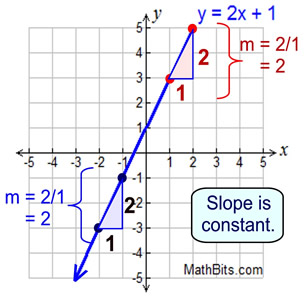
A special circumstance exists when working with straight lines (linear functions), in that the "rate of change" (the slope) is constant. No matter where you check the slope on a straight line, you will get the same answer.
|
|
When you find the "rate of change" you are finding the rate at which (how fast) the function's y-values (output) are changing as compared to the function's x-values (input).
|
The rate of change for a line is the slope, the rise over the run,
the change in y over the chnage in x, or the "m" in y = mx +b. |
|
You should be able to find the rate of change (the slope):
1. by calculations from two points in a table.
2. from the slope as determined on a graph using a right triangle.
3. from a given equation of the line using y = mx + b ("m" = slope).
|
See examples below.

 Finding the rate of change from a table. Finding the rate of change from a table.
A function is shown in the table at the right.
Find the rate of change over associated with this linear function.
Solution:
Choose any 2 points. We are choosing (1, 3) and (3,11).
Substitute into the formula:

The rate of change is 4.
|
|
The y-values change 4 units every time the x-values change 1 unit, on this line. |

 Finding the rate of change from a graph. Finding the rate of change from a graph.
A linear function is shown in the graph at the right.
Find the rate of change for this straight line.
Solution:
Find two points on the line that have integers for their ordered pairs. We are choosing (-2,2) and (2,0).

Or, substitute into the formula:
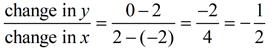
The rate of change is -1/2.
|
|
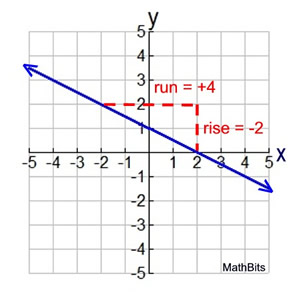
The y-values change -½ unit every time the x-values change 2 units, on this interval.
The negative sign is indicating that the line is decreasing (going down from left to right) on the graph.
|

 Finding the rate of change from an equation. Finding the rate of change from an equation.
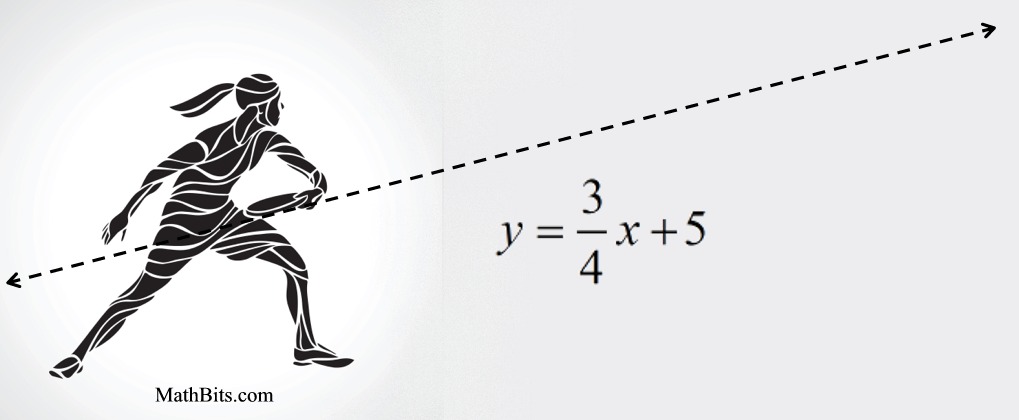
A Frisbee is thrown along a straight line y = ¾ x + 5, where y = the height in feet of the Frisbee above the ground, and x is the time in seconds.
a) What are the units of measurement for the rate of change in the height?
b) Find the rate of change along this line?
|
Solution:
a) Since the rate of change is the "change in the y-values" over the "change in the x-values", the numerator (top) is measured in feet and the denominator (bottom) is measured in seconds. This ratio is measured in feet per second, which will be the velocity of the Frisbee.
b) Remember that the rate of change on a straight line is constant and is represented by the slope of the line. The rate of change is ¾ feet per second.
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|