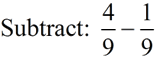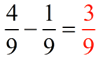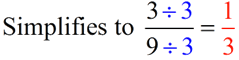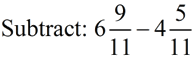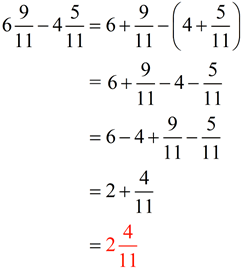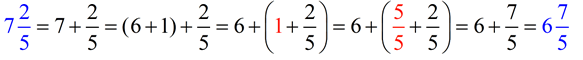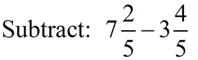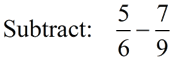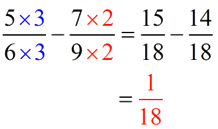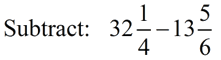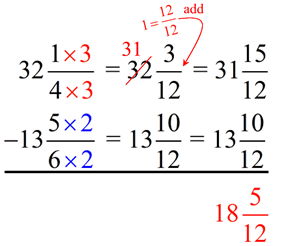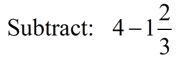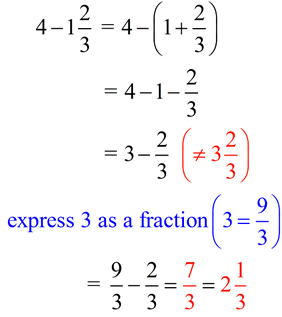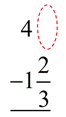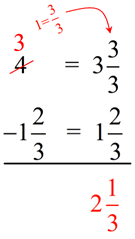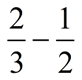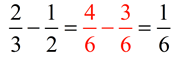|
 |
Rules for Subtracting fractions:
1. The bottom numbers (denominators) must be the same.
2. Subtract the top numbers (numerators)
Put this answer over the denominator.
3. Simplify the fraction, if possible.
Remember: "common denominators"
("common denominators" means the "same" denominators) |
Same Denominators:
"Common Denominators" |
|
When the fractions have the same denominators, adding and subtracting are easy.
|
When adding (or subtracting) fractions with the same denominators,
just add (or subtract) the numerators.

|
When fractions have different denominators, you must work with common denominators. |
When adding (or subtracting) fractions with different denominators,
you must find a common denominator before adding (or subtracting).
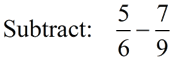
Least common denominator of 6 and 9 is 18.
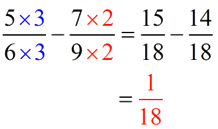 |
|
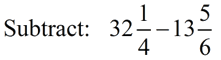
Least common denominator of 4 and 6 is 12. Borrowing will be needed.
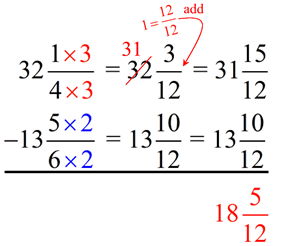
|
|
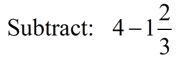
 This type of problem can be confusing. Think carefully before writing your final answer. This type of problem can be confusing. Think carefully before writing your final answer.
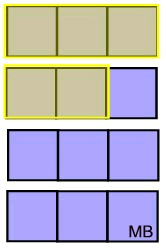
First, let's LOOK at what the answer should be with a visual model.
|
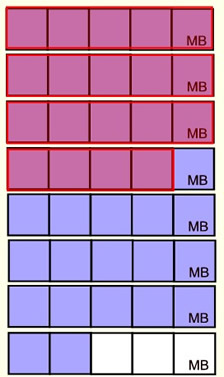
Take away the brown squares.
The answer
should be
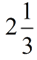 . .

|
|

|
"Separate parts horizontally method":
For this question, this method can be a bit confusing. Be careful!
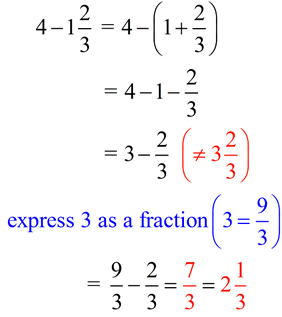
"Line up vertically" method:
This method gives you a bit of a hint that something is missing in this problem. Be careful not to simply "drop" the 2/3 down into the answer.
|
You could think of the empty
oval as
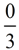 . .
|
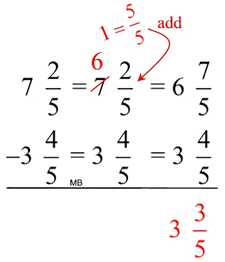
| We need to "borrow" 1 from the 4:
|
|
|
|

Subtracting Fractions on the Number Line: |
Under the Addition of Fractions, we saw how placing the fractions on number lines necessitated determining an equal number of subdivisions for both lines. That same approach applies when working with subtraction.
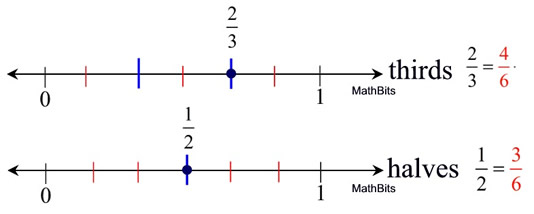
On the "thirds" line, if we cut each "third" into two equal sections we will get 6 in total.
On the "halves" line, if we cut each "half" into three equal sections we will get 6 in total.
(This number 6 will be called our common denominator.)
Subtract:
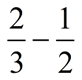 |
|
Now that both lines contain subdivisions of the same size (both have 6 sections), we can express our fractions using this new subdivision size of 1/6. Then we can subtract the fractions.
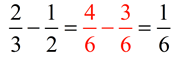
Let's combine our number lines onto one line to demonstrate this difference.
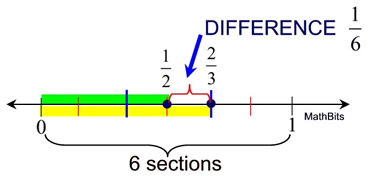

|
For help with fractions
on your calculator,
click here. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|