|
|
Rules for Multiplying fractions:
1. Multiply the top numbers (numerators)
2. Multiply the bottom numbers (denominators).
3. Simplify the fraction, if possible.
"Don't you just LOVE multiplying fractions.
It is soooooo easy!
No common denominators. YEA!
"
|
|
When you multiply two fractions, you simply multiply the numerators (tops)
and you multiply the denominators (bottoms). That's it!
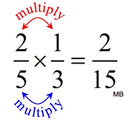
 Multiplying examples: Multiplying examples:
Visualizing Multiplication |
|
Take a "whole" space and divide it into 3 thirds vertically.
Shade 1/3.
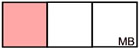 |
Now, divide that same "whole"
into 2 halves horizontally. Shade 1/2.
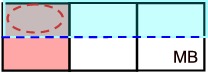 The solution is where the two
The solution is where the two
shadings overlap. It is 1/2 of 1/3.
One of the 6 cells is the solution. |
|
|
Take a "whole" space and divide it
into 5 fifths vertically. Shade 3/5.
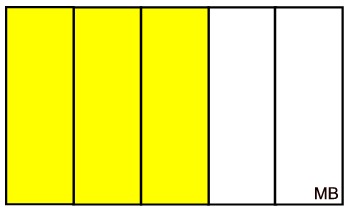 |
Now, divide that same "whole" into
4 fourths horizontally. Shade 3/4.
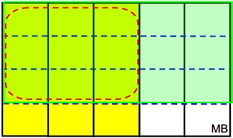 The solution is where the two shadings overlap. It is 3/4 of 3/5.
Nine of the 20 cells are the solution.
The solution is where the two shadings overlap. It is 3/4 of 3/5.
Nine of the 20 cells are the solution. |
|
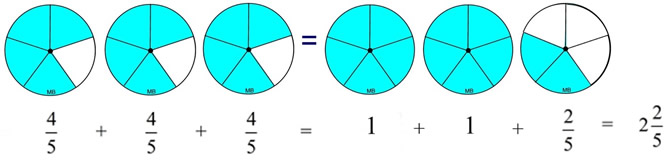
Multiplying by a whole number.
When multiplying a fraction by a whole number,
the multiplication can easily be seen as repeated addition.
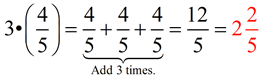
 |

Multiplying Fractions on the Number Line: |
Step 1: Start by plotting 1/2. Since we need to find "2/3 of the distance to 1/2" (or "2/3 of the way to 1/2"), divide the distance from 0 to 1/2 into thirds. We can now visualize this distance. But we don't know the actual length of this distance in terms of the whole from 0 to 1.
Answer: Since the "whole" is represented as the distance from 0 to 1, 2/3 of the distance to 1/2 is 2/6 of the whole.
Of course, this can also be simplified to 1/3 of the whole. |
|
Step 2: Divide the other 1/2 section of the line also into thirds. The entire "whole" from 0 to 1 has now been divided into 6 equal sections. Label each of the sections in "sixths". The answer is that "2/3" of the distance to 1/2" is "2/6 of the distance to 1", or is ""2/6 of the whole".
|
|

|
For help with fractions
on your calculator,
click here. |
|
|