| |
Rules for Dividing fractions:
1. Flip the second term over (this is now the reciprocal)
2. Multiply the first fraction time this reciprocal.
3. Simplify the fraction, if possible.
|
|
Like multiplying, division of fractions is easy!!
To
divide two fractions, you start by fliping over the second fraction
(the one you are dividing by).
Then you muliply the first fraction by this flipped over fraction.
Simplify the answer if needed.
 |
The reciprocal of a fraction is just switching the numerator
(top number) and the denominator (bottom number).
"Reciprocal" is the name given to the flipped over fraction. |
|
 Division examples: Division examples:
1. Whole number divided by fraction:
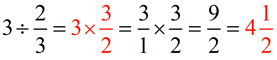 |
2. Fraction divided by a whole number:
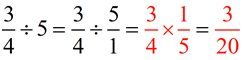
|
3. Fraction divided by fractions:
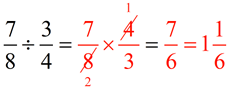
|
4. Fraction divided by mixed number:
Remember to change the mixed number to an improper fraction so you will be able to find the reciprocal.
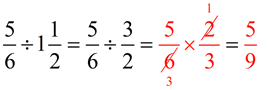 |
5. Mixed number divided by mixed number:
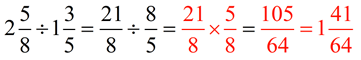 |
6. Mixed numbers divided by a whole number:
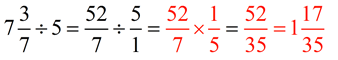
|

(First an easy one, and then a harder one.)
|
We are going to translate this problem as:
"How many 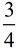 sections can be created from sections can be created from 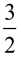 ?" ?"
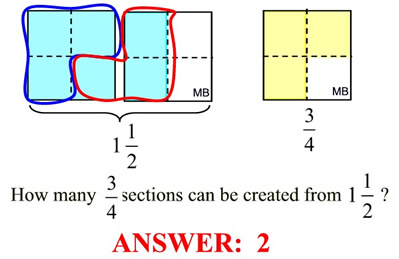
|
|

Division of Fractions on the Number Line |
(First an easy one, and then a harder one.)
|
We are going to translate this problem as:
"How many 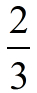 sections can be created from 4?" sections can be created from 4?" |
Set up a number line divided from 0 to 6.
Subdivide each of the full unit sections into 3 equal parts, creating 1/12 sections.
Mark off ONE "2/3 section".
Continuing marking off "2/3 sections" across the number line.
You will notice that the last section ends exactly on the number 4.
Count up the number of "2/3 sections" you were able to mark off.
ANSWER: The number of 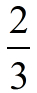 sections that can be created from 4 is 6. sections that can be created from 4 is 6.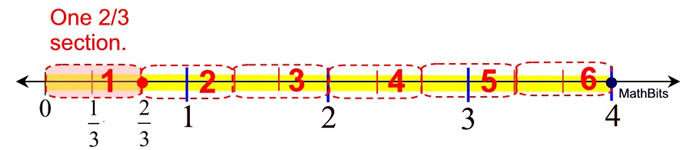
|
|
|
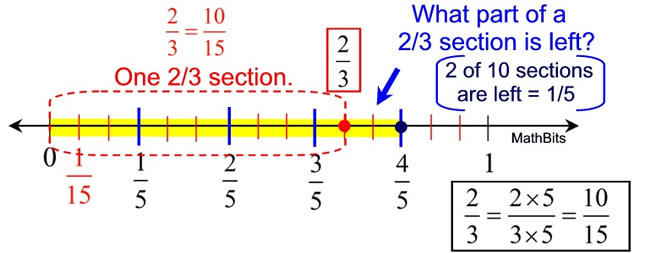
We are going to translate this problem as:
"How many 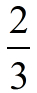 sections can be created from sections can be created from 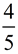 ? " ? " |
Set up a number line with subdivisions of 1/5 and locate 4/5.
Determine the common denominator for 5 and 3, which is 15.
This will tell us the size of a subdivision
shared by both values.
Subdivide each of the 1/5 sections into 3 equal parts, creating 1/15 sections.
Since 2/3 = 10/15, mark off ONE "2/3 section".
Notice that we have two 1/15 sections remaining.

We need to ask "what part of a 2/3 section are these 2 remaining sections?"
What part of 10 is 2? It is 2/10 or 1/5.
ANSWER: The number of 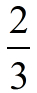 sections that can be created from sections that can be created from 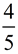 is is 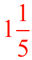 . .

|
|

Where Did This "Flip Over" Process for Dividing Come From? |
Let's review what we know about division.
Division and multiplication are opposite operations. There is an inverse relationship between multiplication and division. The following statement can be made about this relationship:
If a x b = c, then c ÷ a = b or c ÷ b = a.
If c ÷ b = a, then a x b = c or b x a = c.
(for a and b ≠ 0)
|
In plain English:
|
One operation can "undo" the other.
6 x 8 ÷ 8 = 6 x 1 = 6 |
This inverse relationship carries over into the multiplication and division of fractions.
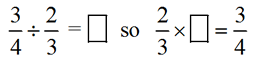
But how do we find that missing number? How do we divide fractions?
Before we answer these questions, we must agree on the following rule:
RULE: 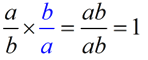 for a ≠0 and b ≠0. for a ≠0 and b ≠0. |
(Note: b/a is called the reciprocal of a/b)
Example: 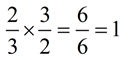 TRUE! TRUE!
Now, we will rewrite our division problem using a fraction bar instead of a division symbol (÷). This "fraction over fraction" form is called a complex fraction, where the numerator is a fraction and/or the denominator is a fraction.
Next, we are going to simplify the denominator by converting that fraction to "1". We will be using the rule stated above with a reciprocal value of 3/2. Remember that we will need to multiply both the top and bottom of the complex fraction by 3/2, so as not to change the value of the entire fraction.
Notice how this process creates a nice, simple denominator of 1. Yea!
Now, just complete the multiplication and arrive at the answer.
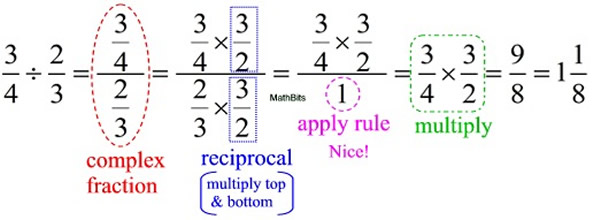
Wow!! That was nice, but rather long. Let's fast forward and examine the process starting with the problem and going directly to the "multiply" step near the end. There is a pattern here!
|
Observations:
• the signs changed from divide to multiply
• the second fraction was written as its reciprocal
Short Cut Method for Dividing:
... take the reciprocal of the second fraction, and multiply. |
|
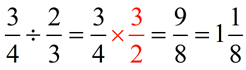

|
For help with fractions
on your calculator,
click here. |
|
|