We know that the fraction ¾ can be read as "3 divided by 4".
If we transfer this to notation, we have:
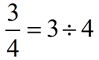
It is also possible to see problems involving division of fractions written with a fraction bar instead of a division symbol ( ÷ ). This "fraction within a fraction" form of expression is called a complex fraction.
 |
A complex fraction is a fraction that has a fraction (or mixed number)
in either the numerator, the denominator, or both. |
|
Yes, complex fractions are a bit scary looking!
The word "complex" in "complex fraction" means multifaceted.
 Normal form of division of fractions.
Normal form of division of fractions. |
|
 Division written in complex fraction form.
Division written in complex fraction form. |
|
 |
When you see one of these "piled up fractions" problems,
remember that the fraction bar means DIVIDE!
Rewrite the problem using a regular division symbol (÷).
All complex fractions can be re-written as division problems.
Remember: the fraction bar means "divided by". |
Complex fractions should be simplified.
To simplify a complex fraction means to write the expression without a fraction in its numerator and/or its denominator. |
There are two methods that can be used to simplify complex fractions.
Method 1: Simplify complex fractions by using division (from the fraction bar).
Method 2: Simplify complex fractions by multiplying by a common denominator.
 Method 1: Simplify complex fractions by using division. Method 1: Simplify complex fractions by using division.
This is the easiest method to remember. Simply interpret the main fraction bar to mean "divided by" and then follow the rules for division of fractions. Life will be easier if you convert both the top fraction and the bottom fraction into "single" fractions (if needed) before dividing.
STEPS:
• Create one single fraction in the numerator (if necessary).
• Create one single fraction in the denominator (if necessary).
• Remember the main fraction bar means "divide". Rewrite the fraction using the ÷ symbol.
• Follow the normal rules for dividing fractions: invert the second term (the denominator of the complex fraction) and change the sign to multiply.
• Simplify whenever possible.
Example:
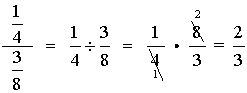 |
Remember, when dividing fractions, invert (flip over, take reciprocal of ) the second fraction and multiply.
Reduce the final answer if needed (or reduce as you multiply). |
|
 Method 2: Simplify complex fractions by multiplying by a common denominator. Method 2: Simplify complex fractions by multiplying by a common denominator.
In this method, EVERY term gets multiplied by the common denominator of all of the fractions.
STEPS:
• Find the least common denominator (LCD) for all fractions appearing within the complex fraction.
• Multiply both the numerator and the denominator of the complex fraction by this LCD.
• Simplify whenever possible.
Example:
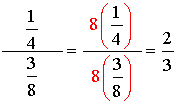 |
The least common denominator for the two fractions in this problem is 8.
Multiply the top and bottom by 8.
|
|

 Complex fractions may appear in various forms: Complex fractions may appear in various forms:
(Method 1 is being used to solve these problems.)
Both the numerator and denominator contain a fraction:
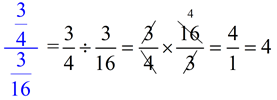
|
The numerator is a whole number and the denominator is a fraction. Expressing the whole number as a fraction (over 1) may help visualize the problem.
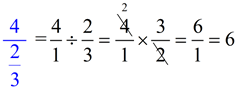 |
The numerator is a fraction and the denominator is a whole number. Expressing the whole number as a fraction (over 1) may help.
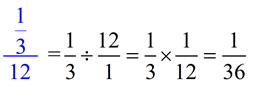 |
A complex fraction may contain a mixed number. Change the mixed number to an improper fraction before solving.
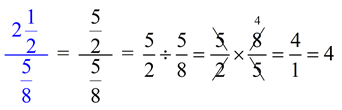 |
A complex fraction may contain expressions. If this happens, combine the expressions into a single fraction before solving.
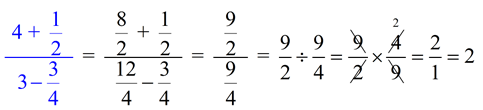 |


|
For help with fractions
on your calculator,
click here. |
|
|