Equivalent Fractions:
Equivalent fractions are fractions that represent the same quantity. |
|
In the following squares, the shaded area remains the same, but the number of sections increases. Notice what is happening to the fractions.
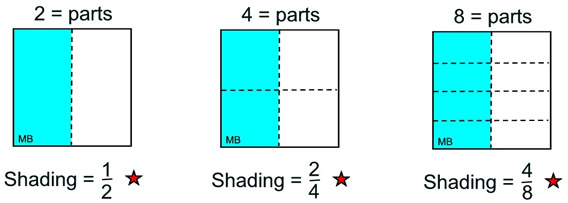
This illustration shows that 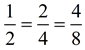 represent the same shaded portion of the square, represent the same shaded portion of the square,
making these equivalent fractions.
| Notice: If you multiply (or divide) the numerator (top) and the denominator (bottom) of a fraction by the same number, you will create a new fraction that is equivalent (equal) to the original fraction. |
|
Example: MULTIPLY
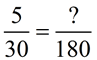
Notice in the denominators a multiple of 6.
Doing the same to the numerator will give the answer.
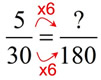
Answer: ? = 5 x 6 = 30 |
|
Example: DIVIDE
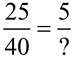
Notice in the numerator a division by 5.
Doing the same to the denominator will give the answer.
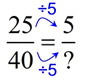
Answer: ? = 40 ÷ 5 = 8 |
|
Fundamental Law of Fractions: the value of a fraction does not change when its numerator and denominator are both multiplied by the same number (not zero).
[Remembering that multiplication by ½ can also be considered division by 2, this law also extends to "division".]

|

Simplifying Fractions:
Reducing Fractions |
|
When working with fractions, it is a common practice to list fractional answers in their "simplest form". The simplest form usually gives the reader a better idea of what the fraction represents.
To simplify (or reduce) a fraction, look for a number that will divide exactly into BOTH the numerator and the denominator. Try to find the "largest" such value (the greatest common divisor).
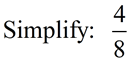
The largest number that will divide exactly into 4 and 8 is 4.
The greatest common divisor (GCD) is 4.
|
The simplified answer is ½. There is no further number that can be used to reduce ½, so you are done. |
|
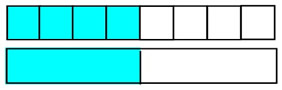 4 "one-eighth" sections of a whole is the same as 1 "one-half" section of the same whole.
4 "one-eighth" sections of a whole is the same as 1 "one-half" section of the same whole. |
|
 |
What happens if you don't think of using
4 as the largest value for division?
Instead you use 2. |
|
|
NO PROBLEM! (But it will require a little bit more work.)
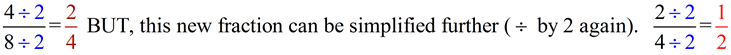
If you don't choose the LARGEST common factor (the GCD), you can still reduce (or simplify) the fraction, but you will have to do the division process more than one time.
When looking for possible factors, keep in mind that:
1. if both numbers are even, they are divisible by 2.
2. if both numbers end in 0 and/or 5, they are divisible by 5.
3. if both numbers end in zeros, they are divisible by 10.
4. if both numbers are such that the sum of the digits of the number
is divisible by 3,
then the numbers are divisible by 3.
5. if
both numbers end in 25, 50, 75 or 100, they are divisible by 25. |
We can state this process of reducing fractions in a generalized form:

|
 |
If a fractional answer can be simplified, the "best" answer is usually the simplified form.
Always follow the directions given in the problem, or by your teacher, as to whether the simplified fraction is required. An un-simplified answer is a "correct" answer unless the question (or your teacher) states that the answer is to be expressed in simplest form.
|
|

Less Than, Greater Than, Equal To:
Comparing fractions as to their size. |
|
 Simple Cut-up Visual Comparisons: Simple Cut-up Visual Comparisons: |
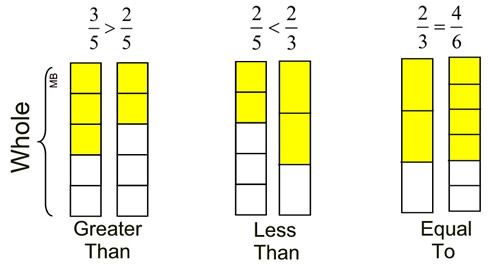
These diagrams show a pictorial representation of what is occurring in relation to the size of the fractions. Each of the whole bars are divided into 5, 3, or 6 equal pieces and compared. Unfortunately, it can be difficult to compare fractions in this simple cut-up visual manner. If we did not know that 2/3 = 4/6 in the last comparison, it would be difficult to tell from the diagram whether the fractions were equal or just really close to being equal.
Let's look at other ways of making comparisons.
 Compare using a Common Denominator: Compare using a Common Denominator: |
1. Comparing fractions that already have the same denominator is easy. The fraction with the larger numerator will be the larger fraction. Since the denominators are the same, you are comparing "pieces" (parts) of the same size. In this example, all of the "pieces" are 1/5 of the whole. So 4 such pieces will be greater than 2 such pieces.
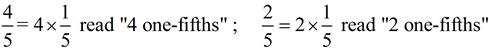
|
|
2. Comparing fractions that have different denominators is harder. The solution requires that we create equivalent fractions that have the same denominators and then compare them. When looking for this same denominator (called the common denominator), look for the smallest possible number (called the least common multiple or the least common denominator) to keep the calculations as simple as possible.
If we re-examine our visual models from above, we can see that when the whole bar is divided equally for BOTH fractions, using the common denominator, we have a more reliable and accurate portrayal of the fraction sizes.
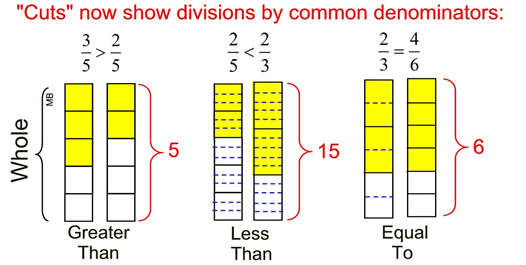
Now, let's determine the comparsion of fractions using a common denominator without the use of a diagram. |
Example: >, <, or =
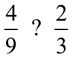
Start with the larger denominator and keep looking at multiples until you find one into which the other denominator will divide exactly (is a factor).
This problem is easy, as the 9 is the larger denominator and 3 will divide exactly into 9.
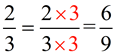
Since the numerator of 6 is larger than the numerator of 4 (when the denominators are the same), 4/9 is smaller than 6/9. Since 6/9 = 2/3, 4/9 is also smaller than 2/3.
Answer:
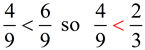
|
|
Example: >, <, or =
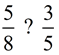
We need to find a value into which both 8 and 5 can divide exactly. We are looking for the least common multiple of 8 and 5 (the LCM). Start with the larger denominator and examine multiples until you find one that also has 5 as a factor.
Multiples of 8: 8, 16, 24, 32, 40 Stop!
5 is a factor of 40.
Use 40 as the common denominator.
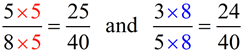
Answer:
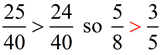 |
|
Example: >, <, or =
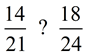
This is a difficult problem. But maybe these fractions can be simplified first, which would make our work easier.
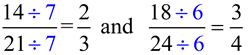
Now, these fractions are easier to manipulate with a common denominator of 12. Multiply 2/3 top and bottom by 4. Multiply 3/4 top and bottom by 3.
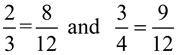
Answer:
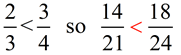 |
|
If you need a common denominator, and you cannot seem to find one, you can always multiply the two denominators that you have to get a common denominator. (Adjust the numerators accordingly.) This may create a little extra work in some cases (such as the example on the left), but it will always work!
 |
|
 Compare using the Cross Multipy Rule: Compare using the Cross Multipy Rule: |
We saw in Ratios and Proportions that the Cross Multiplication Algorithm (Rule) was the result of rewriting fractions to have the same denominator and then comparing the numerators.
The rule states:
We can use this same rule to "compare" fractions.
Here's how this process works:
To compare two fractions,
1. multiply the numerator from the fraction on the left by the denominator of the fraction on the right.
2. Place this number above the fraction on the left.
3. Now, multiply the denominator from the fraction on the left by the numerator of the fraction on the right.
4. Place this number above the fraction on the right.
5. Place the appropriate inequalitiy symbol (< , >, or even =)
As with the Cross Multiplication Algorithm (Rule), this cross multiply application to comparing fractions is actually the result of rewriting fractions to have the same denominators (which we do not write down) and then comparing the numerators.
This is a "short-cut" process where we just don't write down everything that is happening! |
With is process in mind, we can amend the Cross Multiply Rule to include:
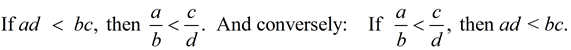 These statements can also be written with " >" replacing " < " in the statements.
These statements can also be written with " >" replacing " < " in the statements. |
|
 Ordering Fractions: Ordering Fractions: |
Place in ascending order (from smallest on the left to largest on the right):
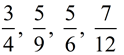
Solution:
We need a common denominator for all four fractions. Yeek!
We will try to save ourselves some work by looking at the prime factorizations of the denominators to look for the LCM.
|
Our common denominator will be 36. 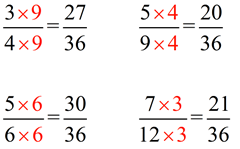 |
In ascending order, we now have: (look at the blue numerators for the ordering)
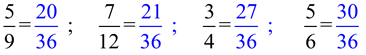
ANSWER:
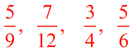

|
For help with fractions
on your calculator,
click here. |
|
|