"So, how difficult is this going to be?"
Yes, word problems can be challenging, and sometimes tricky,
but we will keep this as simple as possible.
Just remember to:
1. Read carefully.
2. Apply your math skills.
(Yes, you have them!)
3. Use your common sense.
|
 |
This page will be dealing with word problems associated
with GCF and LCM. |
|

For the examples on this page, ONE method of solution will be given. Other options may be possible.
Greatest Common Factor (GCF) Word Problems:
These problems tend to follow certain patterns. They typically are associated with concepts such as:
1. share or distribute things equally
2. split things into smaller equal sections
3. determine how many people to invite
4. all things being used, no leftovers
5. arrange into rows or groups
6. using words like
greatest, largest |
1. "Split into smaller equal sections"
Kyle has two tarps that are 84 inches wide and 96 inches wide. He wants to cut them into strips of equal width that are as wide as possible. How wide should he cut the strips from each tarp?
Solution: Since the "widest" and "split things" concepts are present, this is a GCF problem.
Using prime factorization on 84 and 96, find the GCF:
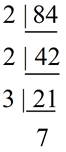 |
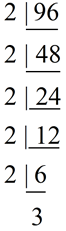 |
84 = 2 x 2 x 3 x 7
96 = 2 x 2 x 2 x 2 x 2 x 3
GCF = 2 x 2 x 3 = 12
Kyle should cut each tarp into 12 inch widths.
FYI: If you look at 84 + 96 = 12(7 + 8)
The GCF is 12. The (7 + 8) tells you to cut 7 strips in the 84" tarp and 8 strips in the 96" tarp.
|

2. "Share or distribute things equally"
Sandy made 45 peanut butter dog treats and 75 chicken dog treats for the animal shelter. She wants to divide the treats so that they are all used, and that the same number of treats are in each baggie. What is the greatest number of baggies she can prepare? How many of each treat are in each baggie?
Solution: Since "all are being used", "distributed evenly", and "greatest" are the key concepts, this is a GCF problem.
Using prime factorization on 45 and 75, find the GCF:
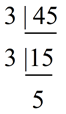 |
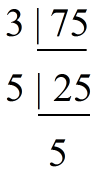 |
45 = 3 x 3 x 5
75 = 3 x 5 x 5
GCF = 3 x 5 = 15 |
You might also want to consider:
45 + 75 = 15(3 + 5)
Where 15 is the GCF,
and 3 and 5 are the numbers
of each of the treats per bag.
|
The GCF represents the number of baggies Sandy can make (15 baggies).
The leftover prime numbers of 3 for 45, and 5 for 75, tell us that each baggie will contain 3 peanut butter treats and 5 chicken treats. |

3. "Arrange in Rows"
There are 64 girls and 72 boys in the marching band. The band director plans a half-time show for the upcoming football game where he will have rows of only girls and rows of only boys marching. What is the largest number of students that could be in each row?
Solution: Since "each row composed of only one gender" and "largest" are the key concepts, this is a GCF problem.
Using prime factorization on 64 and 86, find the GCF:
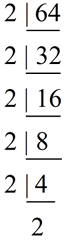 |
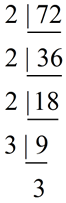 |
64 = 2 x 2 x 2 x 2 x 2 x 2
72 = 2 x 2 x 2 x 3 x 3
GCF = 2 x 2 x 2 = 8 |
You might also want to consider:
64 + 72 = 8(8 + 9)
Where 8 is the GCF (the number of students in a row),
and 8 and 9 are the numbers
of rows of girls and number of rows of boys. |
The GCF represents the number of students per row. (8 students).
FYI: The leftover prime numbers of 8 for 64, and 9 for 72, tell us that 8 of the rows will be girls and 9 of the rows will be boys. |

Let's take minute to review the relationship between GCF and LCM.
We are examining the numbers 24 and 30.
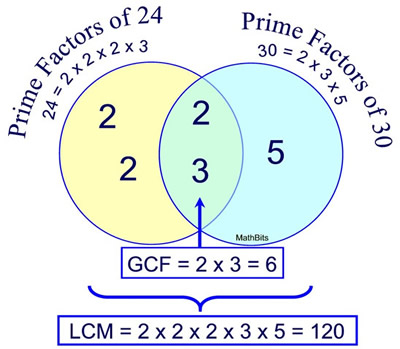 |
The prime factors of each number are assigned to a circle.
Where the factors overlap (are in common) is the section labeled the GCF.
The full number of factors needed to include both sets of factors is labeled the LCM.
The LCM includes factors that did not make it into the GCF. These are often referred to as the "leftovers". |

Least Common Multiple (LCM) Word Problems:
Like the GCF, these LCM problems also tend to follow certain patterns. They typically are associated with concept such as:
1. repetition, an event happening over and over
2. cycle, when will it happen again, at the same time
3. purchase of multiple items to have enough
4. using words like least, smallest |
4. "purchase of multiple items to have enough"
Diana needs to buy beads for her Girl Scout troop. The glass beads come 25 to a package and the wooden beads come 35 to a package. What is the least number of packages she will need to buy to ensure that each of the girl scouts gets the same number of glass beads and the same number of wooden beads?
Solution: Since "purchase of multiple items to have enough" and "least" are the key concepts, this is a LCM problem.
Method 1: Listing multiples
Multiples of 25 are 25, 50, 75, 100, 125, 150, 175, ... (7 bags)
Multiples of 35 are 35, 70, 105, 140, 175, ... (5 bags)
The LCM is 175.
Method 2: Using prime factorization
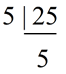 |
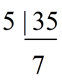 |
25 = 5 x 5
35 = 5 x 7
LCM = 5 x 5 x 7
LCM
= 175
|
Diana needs 175 of each type of bead.
She needs 7 bags of glass beads
and 5 bags of wooden beads.
|

5. "cycle, when will it happen again, at the same time"
Leon's training schedule has him working out in the gym for 14 days before taking a day off. Karla's training schedule has her working out in the gym for 10 days before taking a day off. How many days will it be before they will have a day off together?
Solution: Since "schedule (cycle)" and "before it happens again" are the key concepts, this is a LCM problem.
Method 1: Listing multiples
Multiples of 10 are 10, 20, 30, 40, 50, 60, 70, ... (70 days)
Multiples of 14 are 14, 28, 42, 56, 70, ... (70 days)
The LCM is 70.
Method 2: Using prime factorization
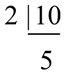 |
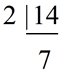 |
10 = 2 x 5
14 = 2 x 7
LCM = 2 x 5 x 7
LCM
= 70
|
It will be 70 days before Leon's day off and Karla's day off coincide.
FYI: At that time he will have completed 5 cycles of his schedule, and she will have completed 7 cycles of her schedule. |
|