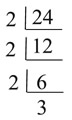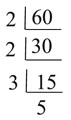 |
A factor of a positive integer is a whole number that divides evenly into the given integer. When you divide by a factor, the remainder is zero.
|
|
Note: Technically, factors of a number can either be positive or negative. We are dealing only with positive factors.
Numerical factoring is the easiest type of factoring because it simply makes a number look like a multiplication problem.
 Factor 24.
If we do simple integer factorization, we can get a series of answers.
| 24 = 1 x 24 |
24 = 2 x 12 |
24 = 3 x 8 |
24 = 4 x 6 |
And of course the order can be reversed (by the commutative property).
| 24 = 24 x 1 |
24 = 12 x 2 |
24 = 8 x 3 |
24 = 6 x 4 |
Factors come in pairs ( 1 & 24, 2 & 12, 3 & 8, 4 & 6). When you divide a number by one of its factors, the answer, or quotient, is the other paired factor.
So which one is the answer to "Factor 24"?
ANSWER: Actually any one, or all, of these listings are the answer.
The answer is usually displayed as a "listing" of all of the factors, such as:
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24 |
|
Integer factorization is the breaking down of a composite (not prime) number into a product
of smaller integers. No specification is necessarily made that the smaller integers must be primes, as is seen in "prime" factorization..
|
|
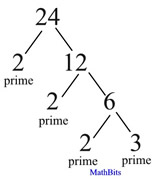
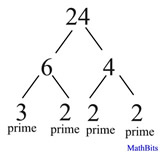
 Find the prime factors of 24?
This problem is a more specific version of Example 1. In this problem, you are being specifically asked for the prime factors of 24, where each of the factors is a prime number. This problem is asking you to perform a prime factorization.
The easiest way to find prime factors is to use a factor tree.
Start dividing with the smallest
possible prime that divides
without a remainder. Continue
until all prime factors are found.
 |
OR, start dividing with any factors that you know for the number. The prime factors will appear.
 |
|
A short hand notation of a factor tree is
a divisional-style listing such as:
ANSWER: The prime factors are
2 x 2 x 2 x 3
or 23 x 3
|
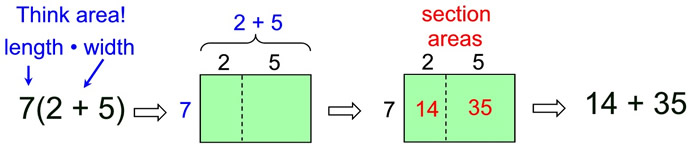
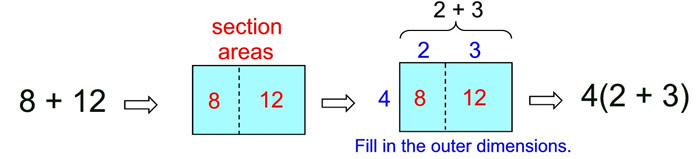
 Write the sum, 24 + 60, as a product of their GCF and another sum.
This problem is a little different than just asking for the factors of a number. In this problem, we will be looking for the largest factor (the GCF) that is shared by 24 and 60. We will then "pull out" this largest factor and place it in front of a set of parentheses surrounding the sum of the remaining factors. This will be the "distributive property" at work.
Looking at a prime factorization of these two numbers will show us what the greatest common factor will be for 24 and 60.
The prime factorization shows us what we have to work with:
  |
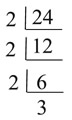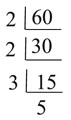Find the prime factors that are
shared by both values:
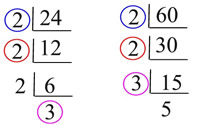
The shared prime factors are 2, 2 and 3, making the GCF 2 x 2 x 3 = 12 |
Now, we need :
24 = 12 x  and 60 = 12 x
Notice that the remaining (unused) prime factors in each of the previous charts will show us the values for the  s.
24 = 12 x 2 and 60 = 12 x 5.
If there is more than one "unused" prime factor left in a chart (or tree), use the product of those unused primes to fill the .
|
Pull the 12 out front
and write the sum of the missing values in the parentheses.
We now have our solution which is:
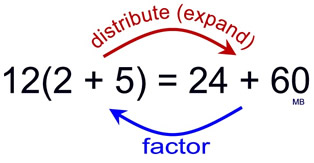
ANSWER: 24 + 60 = 12(2 + 5) |
Use the distributive property to check the answer:
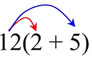
Distribute the 12 across the parentheses.
12 x 2 = 24 and 12 x 5 = 60 |
|
