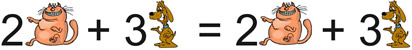|
When working with Algebra, you are primarily working with variables, which can represent known or unknown quantities. The beauty of working with variables, is their ability to represent changing values. Variables, usually designated by letters, will appear along with numbers in algebraic expressions used in a variety of algebraic situations.
 |
Terms are the parts of an expression that are being added and/or subtracted. |
|
|
This expression, 2x + 5, has two terms (2x and 5).
One term (2x) contains a variable, x.
The other term (5) is a number, referred to as a constant.
|
Terms can be a composed of numbers and variables through multiplication
(such as 3x), division (such as b/3), and the use of exponents (such as 3x2).
2x + 5 is not "a term". It is made up of terms. It is an algebraic expression. |
|
Like terms (or similar terms) are terms that represent the same quantities.
In algebra, these terms have the exact same variable component (including the same exponent).
|
|
Consider the statement: Two cats plus three more cats equals a total of five cats.
If we represent "cats" by the letter (variable) "c", we have, 2c + 3c = 5c.
In all three terms, "c" represents the same thing (the species "cat"),
so, the "c's" are referred to as "like" terms.
Since the "c's" are like terms, their quantities can be added together.
Terms that are not "like terms" cannot be added together.
Two cats and three dogs cannot be added together.
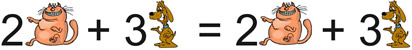
2c + 3d = 2c + 3d
Cats (c) and dogs (d) are not "like" terms, and cannot be added.
Like terms are terms whose variables (including any exponents) are the same.
2x5 and 6x5 are like terms 7a6 and 3a5are NOT like terms
2x5 + 6x5 = 8x5 7a6 + 3a5 = 7a6 + 3a5 (cannot combine)
Note: while an expression such as 3x3 + 2x2 + 5x + 8 uses only the variable letter "x",
we cannot combine these terms because of the exponents involved.
3x3, 2x2 and 5x cannot be added or subtracted.
This expression has 4 distinct terms (3x3, 2x2, 5x, and 8).
Like terms are terms that look like each other.
The only difference will be the coefficients (the numbers in front of the variables).
Like Terms:
|
Notes: |
3, 12, -4, 5x0 |
The simplest "like terms" are numbers (constants).
Remember that the "variable" in a constant term has an exponent of 0, making the variable equal to 1. |
| 3x2 , 6x2 , -2x2 , x2 |
These are "like terms" because each has the variable factor of x2 . |
4a2b3, a2b3, -3a2b3 |
These are "like terms" because each has the variable factor of a2b3. |
Not Like Terms: |
Notes: |
3, 4xy, -2a, 5x2y |
These terms do not have the same variable factor. Remember that xy and x2y are different terms. These examples are unlike terms. |
|
Combining (or Simplifying) Like Terms: |
Like terms can be combined under addition or subtraction.
This process is the same as adding apples to apples, and oranges to oranges.
Just remember to add only the terms that are "like" ("similar").
4a + 5a + a = 10 a 3x - 2x + 4y = x + 4y
When asked to "simplify" an algebraic expression, you are being asked to combine the like terms.
This ability to combine like terms is very helpful when working with both expressions and equations.
Let's try an example ahowing all of the steps:
Simplify: 4x² + 3x³ - 7x + 2x² - 9 + x³ +12x - 11
| 1. Change subtraction to "add opposite" to avoid confusion. |
4x² + 3x³ +(- 7x)+ 2x² +(- 9) + x³ +12x +(- 11) |
| 2. Group like terms. |
3x³ + x³ + 4x² + 2x² +(- 7x) + 12x +(- 9) +(- 11) |
| 3. Add coefficients of like terms. |
4x³ + 6x² + 5x + (- 20) |
| 4. State answer. |
4x³ + 6x² + 5x - 20 |
Examples:
Problem: |
Answer: |
• Simplify: 2x + 4x + x |
Don't forget the implied "1" in front of x.
Think of it as two x's plus four more x's plus one more x.
You can also factor: x(2 + 4 + 1) = 7x
Answer: 7x |
• Simplify: 2x2 + x - 5 + x2 - 4x + 9 |
Group the like terms together and them combine them. Remember when moving terms to move their signs with them. 2x2 + x2 + x - 4x - 5 + 9
Factor: x2 (2 + 1) + x (1 - 4) - 5 + 9
Answer: 3x2 - 3x + 4
|
• Simplify: 6x2 - (10 + 3x2 - 2x) |
Deal with parentheses before you combine the like terms. In this case, distribute -1 across the parentheses. 6x2 -1(10 + 3x2 - 2x)
6x2 -10 - 3x2 + 2x = 6x2 - 3x2 + 2x -10
Answer:
3x2 + 2x -10
|
• Simplify: a2b + 2(3a2b - 5a) |
Distribute the +2 across the parentheses.
a2b + 2(3a2b - 5a) = a2b + 6a2b - 10a
Answer: 7a2b - 10a
|
• Simplify: 5x2 - 4x3 - x2 + 8 |
Look carefully at the exponents.
Answer: - 4x3 + 4 x2 + 8 |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
