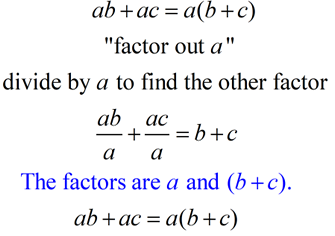|
A factor is a number, or algebraic expression, that divides another number, or expression, with no remainder. On this page, we will concentrate on finding equivalent expressions where one of the expressions is expressed in the form of a product of factors.
We will be looking specifically at "linear expressions".
 |
A linear expression is an algebraic statement where each term is either a constant or a variable raised to the first power. None of the exponents can be greater than 1.
|
|
Examples of linear expressions: 7, 3x, 2m + 5, 4x - 2, 2.3b - 1.2, (½)x + ¼
We will be concentrating on linear expressions that have 2 terms (binomial) or 3 terms (trinomial). In both cases, the highest exponent is one.
Consider the expression (8 + 12):
Numerically speaking: 8 + 12 = 4 ( 2 + 3 )
The greatest common factor of 8 and 12 is 4.
The factors of the expression (8 + 12) are 4 and (2 + 3).

Algebraically speaking:
Looking for the Greatest Common Factor (GCF): |
Let's start by seeing how to find the greatest common factor when working with algebraic expressions. We will be using the concept of prime factorization.
EXAMPLE: Find the greatest common factor of 25x and 15x.
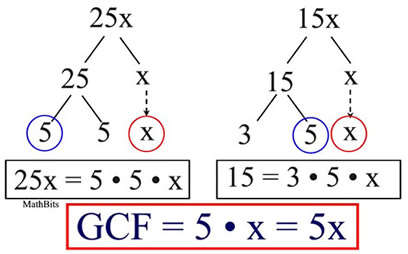
The greatest common factor (GCF) of two single terms is the product of the greatest common factor of the numerical coefficients (the numbers out in front) and the highest power of the variable that is a factor of each term.
|
Find GCF: 18x and 27x
The greatest common factor is 9x.
The largest factor of 18 and 27 is 9.
The variable x (to a power of 1) is a factor in both terms.
|
|
 |
Find GCF: 18x and 27
The greatest common factor is 9.
The largest factor of 18 and 27 is 9.
There is no variable factor since x is only in one term.
|
|
To factor an algebraic linear expression:
• Find the greatest common factor (GCF).
•
Factor out that value by dividing. |

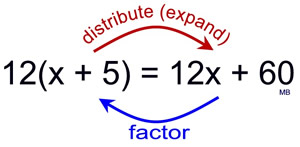
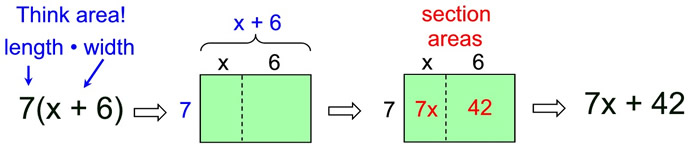
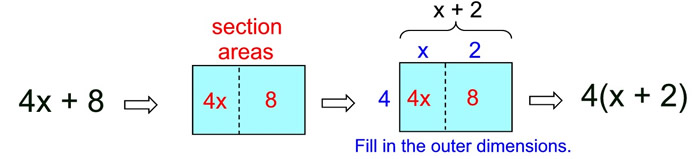
Distributive Property: a(b + c) = ab + ac
Distributive Property in Reverse: ab + ac = a(b + c) |
The distributive property in reverse shows the factoring of an expression.
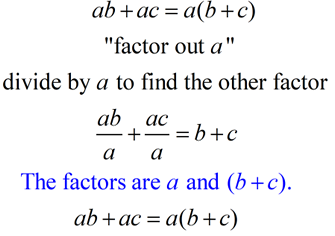
When factoring linear expressions),
first find the GCF,
which is a factor of each term of the expression.
The GCF will be one term (a monomial).
Factor out (divide each term by) this GCF.
The remaining factor will most likely be in parentheses.
Factor: 6x + 42
The largest integer that will divide evenly into 6 and 42 is 6. Since the terms do not have a variable (such as x) in common, we cannot factor any variables.
The greatest common factor is 6. Divide each term by 6.
Answer: 6(x + 7)
Equivalent expressions: 6x + 42 = 6(x + 7)
|

|
|
 |
This result may look familiar. It is the backward version of the Distributive Property (mentioned above). Factoring this expression in this manner, is applying the Distributive Property in reverse (backward). |
Factor: 18x - 27
The largest integer that will divide evenly into 18 and 27 is 9. Since the terms do not contain a variable (such as x) in common, we cannot factor any variables.
The GCF is 9. Divide each term by 9.
Answer: 9(2x - 3)
Equivalent expressions: 18x - 27= 9(2x - 3)
|

|
|
Factor: (¾)a + ¼
The largest value that divides evenly into ¾ and ¼ is ¼. The variable a is NOT present in both terms.
The GCF is ¼. Divide each term by the GCF.
Answer: ¼(3a + 1)
Equivalent expressions: (¾) x + ¼ = ¼(3a + 1)
|

|
|
Factor: 2x + 2y + 1 + 1
This problem is a bit sneaky! Combine terms first.
2x + 2y + 2 This looks better!
The largest integer that divides evenly into 2, 2 and 2 is 2.
There are no variables common to all three terms.
The GCF is 2. Divide each term by the GCF.
Answer: 2(x + y + 1)
Equivalent expressions:
2x + 2y + 1 + 1 = 2(x + y + 1)
|

|
|
Remember that the Distributive Property can be used in a "working backward strategy" to express a linear expression as a product of its factors. A linear expression is in factored form when it is expressed as the product of its factors. |