In Exponent Basics we worked with whole number exponents. The whole numbers are the set of numbers {0, 1, 2, 3, 4, ...}. The whole numbers are the positive integers, plus zero. On this page, we will be examing exponents that are negative integers. {..., -5, -4, -3, -2, -1}. Negative Integer Exponents An value raised to a negative exponent is equal to the number one divided by the value with the sign of the exponent changed to positive. 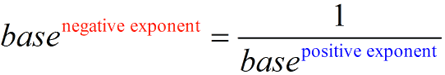For any non-zero number x, and for any positive integer n, 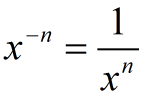There are three important concepts at work in this Rule: For any non-zero number x, and for any positive integer, n: Remember, any number (or expression) with a negative exponent ends up on the opposite side of the fraction bar, with a positive exponent. 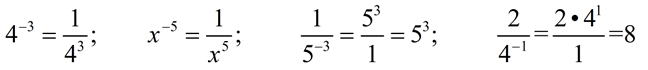The use of a positive exponent is an application of repeated multiplication by the base: 43 = 4 • 4 • 4 = 64. The use of a negative exponent produces the opposite of repeated multiplication. 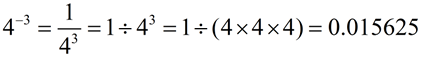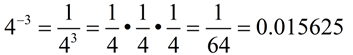It can be thought of as a form of repeated division by the base: 4-3 = 1 ÷ 4 ÷ 4 ÷ 4 = 0.015625 Examples: 1.     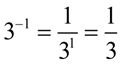The negative 1 exponent indicates that the value is the same as 1 over 3 raised to a power of positive 1.    2.   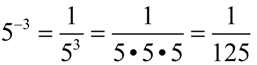3.   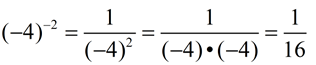Be sure of keep the negative base in the set of parentheses to avoid calculation errors. 4.   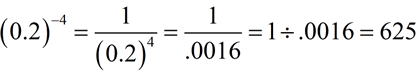This example is working with a decimal base. The same process applies. 5. 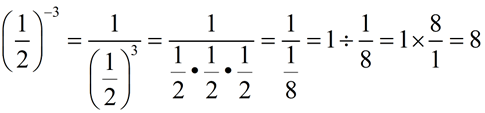Working with a fraction as the base can be more complicated. When applying the process for negative exponents, a "complex" fraction is formed (a fraction within a fraction). Remember that the fraction bar means divide, when rewriting the complex fraction. 6.   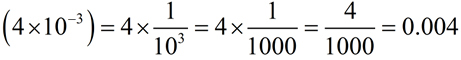This is similar to scientific notation, which would be 4.0 x 10-3. 7.   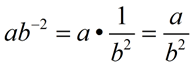Negative exponents can be also used with variables. Just imagine the variable to be a numeric value and apply the process for negative exponents.

Let's take a closer look at why this Rule is true:

One of the Laws of Exponents is that x^m • xⁿ = x^m+n.
"When multiplying exponential expressions, if the bases are the same, add the exponents."

If we apply this law to work with a negative exponent, we get 4³ • 4^-3 = 4^3+(-3) = 4⁰ = 1.
This application shows us that 4³ • 4^-3 = 1, which means that 4^-3 must the multiplicative identity of 4³. Therefore, 4^-3 must be a fraction and it must be the reciprocal of 4³.
Consequently, .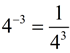

For calculator help with exponents click here.