1. 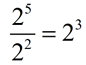
The bases are the same (both 2's), so the exponents are subtracted.
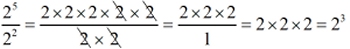
|
2. 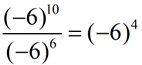
The bases can be negative values.The parentheses tell you that the entire negative value is being raised to the power.
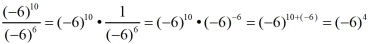
|
3. 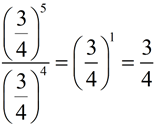
The bases are the same fraction 3/4, so the exponents are subtracted. |
4. 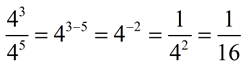
The subtraction is always done "top" minus "bottom" exponents. In this problem we get
3 - 5 = -2. This gives us a negative exponent. Remember, with negative exponents, the answer becomes one over the base with the exponent changed to positive.
|
5. 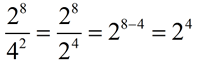
Sneaky one!!!! The bases were not the same in the original problem, but they can be CHANGED to be the same.
4 can be rewritten as 2 squared.
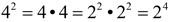 (Multiplication Rule). (Multiplication Rule).
|
6. 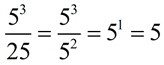
As was done in Example 5, the bottom number is changed to be compatible with a base value of 5.
|
7. 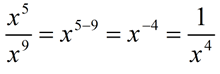
Let's take a look at working with variables. Again, subtraction "top" minus "bottom" exponents. In this problem we get 5 - 9 = -4.
The answer becomes one over the base of x raised to the power of +4.
|
8. 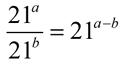
If the exponents are expressed as integer variables, simply apply the rule (subtract the variables) and leave the answer in that form.
|
9. 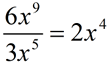
The bases are the same (both x's), so the exponents are subtracted. The numbers in front of the bases (the coefficients) are divided. |
10. 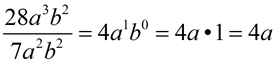
Remember: top exponent minus bottom exponent.
Remember: raising to a 0 power creates a 1.
Divide the integer numbers in front (the coefficients). |