|
We have been working with systems of linear equations where the number of equations (two) is the same as the number of variables (two, such as x and y). With such systems, you will usually find one unique solution. But, there exists a possibility that you may find something else instead.
We have already seen graphical references to the fact that there can be special cases of linear systems. There are actually three possible cases of what may occur when solving a system of linear equations.
 When looking for the solution to a system of linear equations,
you will find one of three possible situations. There will be:
• one solution,
• no solution, or
• infinitely many solutions.
|
GRAPHICALLY:
Solving a system of two linear equations graphically is actually dealing with two straight lines, and how they behave on a graph in relation to one another. The most likely solution is the one point on the graph where the two lines intersect. But ... there are also two other possibilities.
|
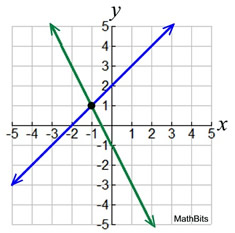 One Solution
The slopes of the lines are different.
One Solution
The slopes of the lines are different.
This is the most common situation.
There will be ONE point of intersection.
|
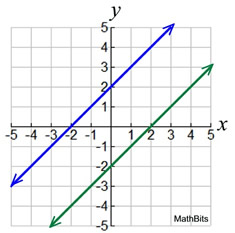 No Solution
The lines are parallel with the same slopes, but different y-intercepts.
No Solution
The lines are parallel with the same slopes, but different y-intercepts.
There will be no intersection of the lines, thus no solution. |
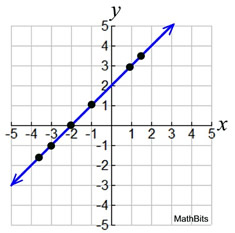 Infinite Solutions
The lines are the SAME line (one on top of the other). The slopes are the same and the y-intercepts are the same. The lines intersect everywhere and ALL points on the line are solutions, so infinitely many solutions.
Infinite Solutions
The lines are the SAME line (one on top of the other). The slopes are the same and the y-intercepts are the same. The lines intersect everywhere and ALL points on the line are solutions, so infinitely many solutions.
|
FYI: Systems that have "no solution" are called "inconsistent systems". Systems with "one solution" are called "independently consistent: systems. Systems with "infinitely many solutions" are called "dependently consistent systems".
ALGEBRAICALLY:
When graphically solving a linear system, it becomes visually obvious what is occurring with the lines and what the solution will be. But, when solving a linear system algebraically, using either the Substitution Method or the Elimination Method, it may not be immediately obvious what is happening. Let's take a look at what may occur.
 What do you see when the solution is "NO Solution"? What do you see when the solution is "NO Solution"?
|
Elimination Method:
| Multiply the first equation by 2: |
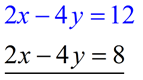
|
Subtract the second equation
from the first equation: |
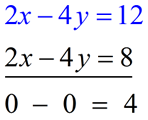 |
Look at the result:
Yes, it looks weird with no variables! AND, the number statement is also FALSE! |
0 = 4 NOT True! |
|
|
There will be "NO SOLUTION" when:
• there are no variables in the answer line, and
• the number statement is FALSE. |
|
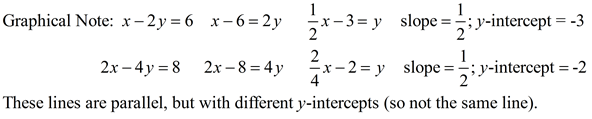
No intersection = no solution.
 What do you see when the solution is "Infinitely many solutions"? What do you see when the solution is "Infinitely many solutions"?
|
Elimination Method:
| Multiply the first equation by 2: |
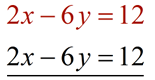
|
Subtract the second equation
from the first equation: |
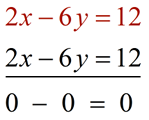 |
Look at the result:
Yes, again, it looks weird with no variables! BUT this time the number statement is TRUE. |
0 = 0 TRUE! |
|
|
There will be "Infinitely many solutions" when:
• there are no variables in the answer line, and
• the number statement is TRUE. |
|
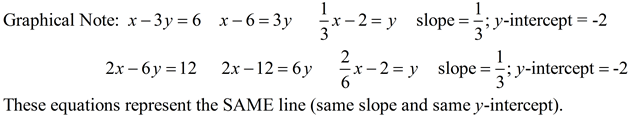
Intersection everywhere = infinite solutions.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|