|
It is possible to solve systems of equations using a table.
The tables may be drawn in a variety of forms and shapes, including tables generated from a graphing calculator.
The table method is a "partner" to the graphical solution.
A table of values is a listing of select points from the straight line graphs.
Where the lines intersect on a graph, the y-values will be the same.
In the tables, we will be looking for the x-location where the y-values are the same.
Example 1:
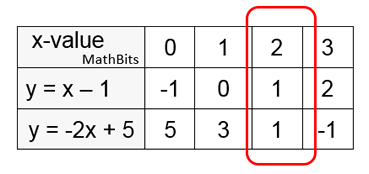
Solve the system y = x - 1 and y = -2x + 5
using a table.
A horizontal table is shown at the right,
containing the two linear equations and a listing of possible x values.
The solution is (x, y) = (2, 1) |
 |
|
In a table solution, x-values are substituted into both linear equations in the system. When the same y-value appears in BOTH equations, the solution has been found. |
|
|
When working with a table solution method,
place both linear equations in "y =" form.
This will make it eeasier to examine the y-values.
|
|
Example 2:
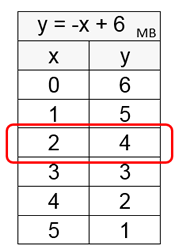
Solve the system x + y = 6 and 2x + y = 8
using two separate tables.
First, put the equations into "y =" form:
y = -x + 6
y = -2x + 8
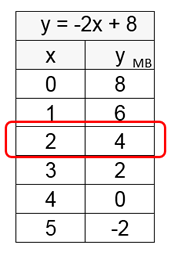
The vertical tables are shown at the right,
containing the two linear equations and a listing of possible x values.
The solution is (x, y) = (2, 4) |
|

Example 3:
Solve the system x - y = -3 and 2x + y = 6
using the graphing calculator table.
First, put the equations into "y =" form:
y = x + 3
y = -2x + 6
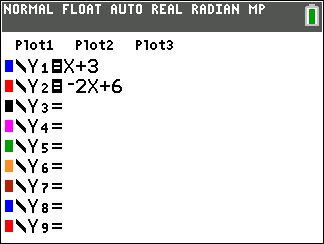
The graphing calculator table is shown at the right, containing the two linear equations and a listing of possible x values.
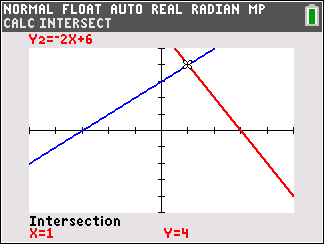
The solution is (x, y) = (1, 4) |
Let Y1 = x + 3 and Y2 = -2x = 6.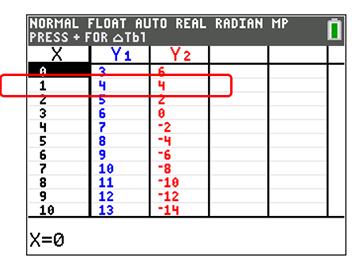
` |
| The screens below do not need to be displayed in a table solution, but they show the equations used to create the table, and that the intersection point (the solution) is at the point (1, 4). |
|
|
|
|
When using the graphing calculator, you will still need to set the equations equal to y before you begin.
Follow the link at the right to see how to use your graphing calculator with systems and how to see the table, and control the table view.
|
|
|
|
For calculator help with systems of equations
click here. |
|
|

What happens with much larger (or much smaller) integer solutions?
If the x-value in the solution is an integer from -4 and +4, it is fairly easy to test each of those 9 values to see which might be the solution. But what if the answer is not an integer in that range? What if the answer is an x-value that is much larger (or smaller)? Is there a way to narrow in on what that value might be?
ANSWER: Let's assume that the x-solution is still an integer, but it is not in the range from -4 to 4. While there is no way to "immediately" find the x-solution using just a table, you can narrow in on the solution, by looking at the difference between the y-values. The difference between the y-values should be getting smaller if you are heading toward the solution. Remember that when using a graph to find the solution to a system, the point of intersection of the lines is the answer. At the point of intersection, the difference between the y-values is 0.
Example 4:
Solve the system y = x + 8 and y = 2x - 4 using a table.
Let's start our table in the positive x direction from 0 to 4.
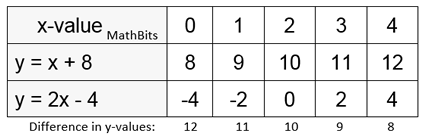
No solution yet! Notice that the difference between the y-values is getting smaller, so we are heading in the right direction, but we need to jump ahead faster (pick some larger values for x). |
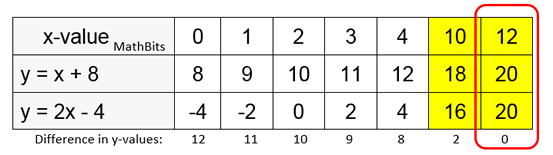
Since the difference of the y-values was decreasing by 1 each time, we can count that we would need 8 more chart entries to get the difference to be 0. Eight more chart entries puts the x-value at 12. Solution (12, 20) |

Example 5:
Solve the system y = x + 8 and y = 2x + 20 using a table.
Let's again start our table in the positive x direction from 0 to 4. 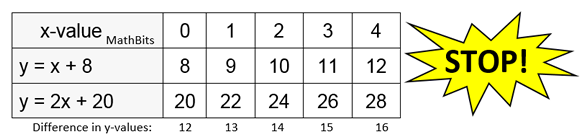
Stop!! The difference in the y-values is getting larger. We are heading in the wrong direction to arrive at the answer. We need our x-value to be going in the negative direction.
Change the direction to have x-values from 0 to -4, for starters.
The difference in the y-values shows we are headed in the correct direction, but we need to move further to the left. Solution: (-12, -4)
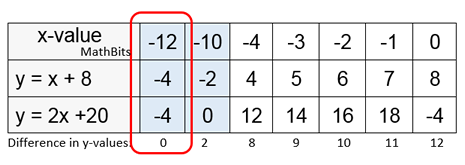

At the beginning of this page, it was stated that tables are "partners" with graphs.
The examples above show some of the problems you can encounter when solving a system of equations using only the table method. These examples all had nice integer answers.
The problems encountered with the table method and rational solutions (including decimals and fractions) arise very quickly. If, however, you "partner" the table method with a graph (even a hand drawn graph), you will have an indication of the approximate location of the intersection (the answer), and you can adjust the table accordingly to narrow in on the solution.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|