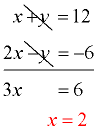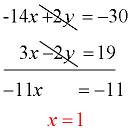|
|
A system of equations is a set of equations that are solved collectively (together). The basic linear system is composed of two linear equations with two variables. Remember that linear equations are equations that represent straight lines when graphed.
The term "simultaneous equations" is also used for "systems of equations". "Simultaneous" means being solved "at the same time". |
There are two basic methods of solving linear systems algebraically:
the Substitution Method and the Elimination Method (Addition/Subtraction Method).
Answers to Systems of Equations may be expressed as a listing of the two variables, such as x = 2 and y = 5, or as an ordered pair (point on a graph)
such as (x, y) = (2, 5). |
 Substitution Method Substitution Method |
The goal of the substitution method is to completely eliminate one of the two variables in the linear system by replacing it with an equivalent expression. This goal is accomplished by solving for one variable from one equation and plugging it into the other equation.
Think of it as "grabbing" what one variable equals from one equation
and "plugging" it into the other equation.

Solve this system of equations and check your solution:
|
2x - y = 0
5x - 2y = 3
|
1. Solve one of the equations for either "x" or "y". Which equation you pick is your choice, but try to pick the easier one to solve.
This example solves the first equation for "y". |
2x - y = 0 (add y to both sides)
2x = y or y = 2x |
| 2. Replace the "y" in the second equation with what you found "y" to equal. Replace "y" with "2x". |
5x - 2y = 3
5x - 2(2x) = 3 |
| 3. Solve this new equation for "x". |
5x - 2(2x) = 3
5x - 4x = 3
x = 3 |
| 4. Substitute this x-value into either of the ORIGINAL equations and solve for "y". Plug into the equation that will solve most easily. |
2x - y = 0
2(3) - y = 0
6 = y |
5. CHECK: Substitute x = 3 and y = 6 into BOTH of the original equations.
If your solutions are correct, both equations will be true!
2x - y = 0
2(3) - 6 = 0
6 - 6 = 0
0 = 0 (check) |
5x - 2y = 3
5(3) - 2(6) = 3
15 - 12 = 3
3 = 3 (check) |
|
 |
|
|
 Elimination Method Elimination Method |
The goal of the elimination method is to create a situation where one set of the variables will cancel each other out when the equations are added or subtracted. It may be necessary, with this method, to create coefficients for these variables that are the same (or negatives), to make the cancellation possible. This creation process is accomplished by multiplying through the equations.
Think of this adding or subtracting method as temporarily
"eliminating" one of the variables to make your life easier.
Solve this system of equations and check your solution: (easy one)
|
x + y = 12
2x - y = -6
|
* Before you begin, be sure the variables and constants are "lined up" one under the other. If needed, rearrange the equations until this occurs. |
1. The variables in this example are already lined up, so let's begin.
Decide
which variable ("x" or "y") will be easier to cancel (eliminate). In order for a cancellation (or elimination) to occur, the coefficients of the variables (the numbers in front of the variables) must be the same or negatives of one another. In this example, the y-values will most easily cancel out one another when the equations are added. |
x + y = 12
2x - y = -6
|
2. Add the equations (add the x's, the y's and the constants.
Watch out for the signs. The y's will be eliminated. Solve for x. |
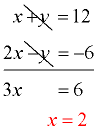
|
3. Substitute x = 2 into either of the ORIGINAL equations and
solve for "y". Choose the equation that will solve most easily. |
x + y = 12
2 + y = 12
y = 10
|
4. CHECK: Substitute x = 2 and y = 10 into BOTH of the original equations.
If your solutions are correct, both equations will be true!
x + y = 12
2 + 10 = 12
12 = 12 (check) |
2x - y = -6
2(2) - 10 = -6
4 - 10 = -6
-6 = -6 (check) |
|
 |
|


Solve this system of equations and check your solution: (harder one)
|
-15 - y = -7x
3x - 19 = 2y |
1. Line up the variables and constants. The equations must be rearranged so this will occur. Try to keep the x and y on one side of the equal sign.
|
7x - y = 15
3x - 2y = 19
|
2. Decide
which variable ("x" or "y") will be easier to cancel (eliminate). In this example, we must make adjustments so that either the x's or y's will cancel. If we multiply the top equation by -2, we will be able to get the y's to cancel when we add. This is the easier method, since if we wanted the x's to cancel we would need to multiply both equations (by 3 and by -7, for example).
Yes, you could also multiply by +2 and then "subtract" the equations. |
-2(7x - y = 15)
3x - 2y = 19
-14x + 2y = -30
3x - 2y = 19
|
3. Add the equations (add the x's, the y's and the constants).
Watch out for the signs. The y's will be eliminated. Solve for x |
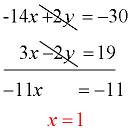
|
4. Substitute x = 1 into either of the ORIGINAL equations and
solve for "y". Choose the equation that will solve most easily. |
3x - 2y = 19
3(1)- 2y = 19
3 - 2y = 19
-2y = 16
y = -8
|
5. CHECK: Substitute x = 1 and y = -8 into BOTH of the original equations.
If your solutions are correct, both equations will be true!
7x - y = 15
7(1) - (-8) = 15
7 + 8 = 15
15 = 15 (check) |
3x - 2y = 19
3(1) - 2(-8) = 19
3 + 16 = 19
19 = 19 (check) |
|
 |
|

In Summary:
Substitution Method
1. Solve for x or y in one equation.
2. Plug into other equation and solve.
3. Use this answer to find other variable by plugging into either equation.
4. Check |
|
Elimination Method
1. Line up equations.
2. Get one variable with same coefficient (leading number) in both equations.
3. Add or subtract to cancel variable. Solve.
4. Use this answer to find other variable by plugging into either equation.
5. Check |
|
|
Yes, these are algebraic solution methods. But, you can still use your graphing calculator to double CHECK your solutions. Click the calculator at the right to see how to use the calculator with systems.
|
|
|
|
For calculator help with systems of equations
click here. |
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|