|
In our study of equations, we have used variables to represent two quantities that change in relation to one another. For example, we can represent a relation such as "y is four more than three times x" by an equation, where the output value of y is determined by the input value of x. The variables in such a relationship statement can be categorized as a dependent variable and an independent variable.

 A dependent variable relies (or depends) on another variable(s) to determine its value. A dependent variable relies (or depends) on another variable(s) to determine its value.
A dependent variable is the "output" value that depends upon the manipulation of an independent "input" variable. |
 An independent variable does not rely (or depend) on another variable(s) to determine its value. An independent variable does not rely (or depend) on another variable(s) to determine its value.
An independent variable is an "input" value that is not affected by changes produced within an equation.
|
For example, in the equation y = 3x + 4, the variable "x" is the independent variable. Once a value for "x" is set, such as x = 12, this x-value will not be "changed" by substituting x = 12 into the equation. The variable "y", however, depends upon what number is substituted for variable x, making y the dependent variable. The "y" variable is being controlled by the value of "x".

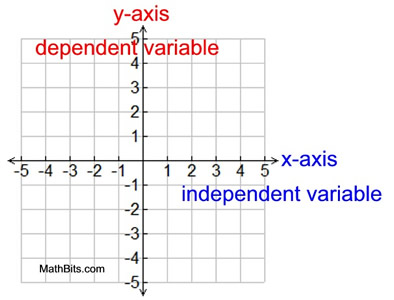
When graphing on a coordinate axis, the independent variable appears on the x-axis
(the horizontal axis), and the dependent variable appears on the y-axis (the vertical axis).
Scientists who deal with data from research and experimentation, often refer to the x-axis (the independent axis) as "the cause", and the y-axis (the dependent axis) as "the effect".
The number from the x-axis "causes" the "effect" (result) seen on the y-axis.
|
 |


Let m = the number of Three Musketeer Candy Bars purchased
Each candy bar costs $1.30
Let C = the total cost of the candy bars purchased
Let's take a look at two different situations that may exist in relation to this information. These situations are based upon what you "know" about this information and what you "want to know".
Situation 1: We know the number of candy bars purchased, m. We want to know the total cost, C, of these candy bars.
Equation: C = 1.30 m
In this situation,
m is the independent variable
C is the dependent variable |
Situation 2: We know how much money, C, we spent on the candy bars. We want to know how many candy bars, m, we purchased.
Equation: 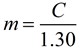
In this situation:
C is the independent variable
m is the dependent variable |


The school dance committee plans to offer refreshments at the homecoming dance. The number of pizzas that are purchased will depend upon the number of students attending the dance.
Let:
s = the number of students attending the dance
p = the number of pizzas purchased
Which of the following statements is true?
1. s is the independent variable and p is the dependent variable
2. p is the independent variable and s is the dependent variable |
|
|