|
 Right Triangular Prism
Right Triangular Prism |
Prisms and Pyramids
Volume is the amount of three-dimensional space an object occupies, in cubic units, within a container.
|
 Right Rectangular Pyramid
Right Rectangular Pyramid |
The volume of a prism is its base area
times its height.
V = volume in cubic units; B = area of the base in square units;
h = prism height in units |
Vprism = Bh |
|
The volume of a pyramid is one-third
the area of its base times its height.
B = base of pyramid, h = height
|
|
|
 Note: Actual dimensions have been rounded to nearest tenth, as needed.
Note: Actual dimensions have been rounded to nearest tenth, as needed.
 (Right Triangular Prism) (Right Triangular Prism)
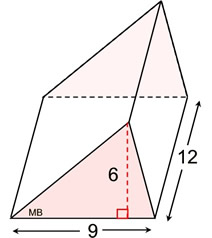
1. Find the volume of this right triangular prism. Remember to show your work.
Solution:
• Find the area of the triangular base.
Since the base is a triangle, use A = ½ b• h.
A = ½ • 9 • 6 = 27 sq. units.
• The prism's height = 12 units.
• The prism volume formula is V = Bh, where B = base area and h = height of prism.
V = 27 sq. units • 12 units
= 324 cubic units. |
 |

 (Right Regular Triangular Pyramid) (Right Regular Triangular Pyramid)
2. Find the volume of this right regular triangular pyramid.
Remember to show your work.
Solution:
• A "regular" triangular pyramid means that all three side of the triangular base are the same length (10 units), making the base an equilateral triangle.
• Find the area of the triangular base. A = ½ b• h.
A = ½ • 10 • 8.7 = 43.5 sq. units.
• The pyramid's height = 12 units.
• The pyramid volume formula is V = (1/3)Bh.
V = (1/3)• 43.5 sq. units • 12 units
= 174 cubic units. |
|

 (Right Trapezoidal Prism) (Right Trapezoidal Prism)
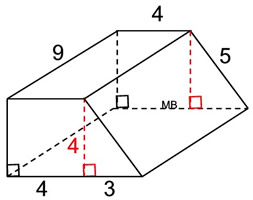
3. Find the volume of this right trapezoidal prism.
Remember to show your work.
Solution:
• Find the area of the trapezoidal base by decomposing the trapezoid.
A (triangle) + A(square) =
½ (3)(4) + (4)(4) = 22 sq. units.
• The prism's height = 9 units.
• The prism volume formula is V = Bh.
V = 22 sq. units • 9 units
= 198 cubic units. |
 |

 (Right Trapezoidal Pyramid) (Right Trapezoidal Pyramid)
4. Find the volume of this right, trapezoidal pyramid.
Remember to show your work.
Solution:
• Find the area of the trapezoid base by decomposing.
A(triangle) + A(rectangle) + A(triangle) =
½ (3)(4) + (4)(8) + ½(3)(4) = 44 sq. units
• The pyramid's height = 12 units.
• The pyramid's volume is V =(1/3)Bh.
V = (1/3) • 44 sq. units • 12 units
= 176 cubic units. |
|

 (Composite Solid) (Composite Solid)
5. Find the volume of this solid, composed of a right square prism and a right square pyramid.
Remember to show your work.
Solution:
• Find the volume of the right square prism.
V = l • w • h = 8•8•8 = 512 cubic units
• Find the volume of the right square pyramid.
V = (1/3)•Bh = (1/3)•(8)(8)•9 = 192 cubic units
• Find the volume of the composite solid.
Add the two volumes.
V = 512 cu. units + 192 cu. units = 704 cubic units. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|