|
|
A composite figure is a geometric figure which is formed by (or composed of) two or more basic geometric figures. |
|
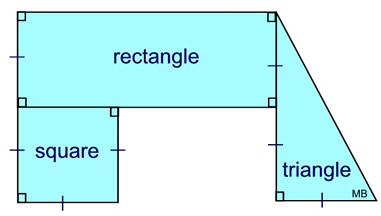
The figure at the right is a composite figure.
It is composed (made up) of a rectangle, a square, and a triangle.
Composite figures may, or may not, show the full outlines of each of their components, as was done in this figure. You can clearly see the three components that made up this figure.
|
 |
Composite figures are usually made up of a combination of triangles, quadrilaterals, and/or other polygons.
|
The area of a composite figure is the total of the areas of the combined shapes that make up the figure. Simply find the area of each shape within the composite. Then add these areas together to get the area of the composite figure.
The original figure at the right contained the right angle markings, hash markings (to show equivalent lengths) and the two lengths written in black (5 ft. and 14 ft). The question asked for the area, in square feet, to be found.
The red lengths and the yellow "areas" were added during the solution to the problem.
Known facts about the 3 shapes, along with computation and hash marks, allowed for the labeling of the red lengths.
|
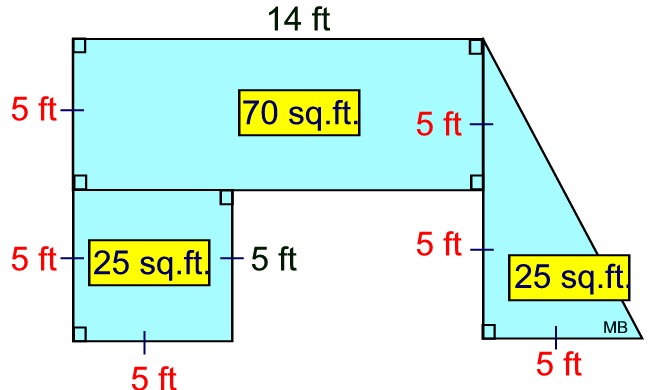 |
The area of the composite figure = area of square + area of
rectangle + area of triangle.
(5 x 5) + (5 x 14) + ½(10 x 5)
Composite Area = 25 + 70 + 25 = 120 sq. ft.
|

 |
This process of breaking a geometric figure up into a series of recognizable figures is known as decomposing.
For example, the trapezoid shown at the left is beiing broken into two right triangles and a rectangle.
While the formula for the area of a trapezoid may be forgotten, the area formulas for triangles and rectangles are more easily remembered.
|
|
Decomposing (or decomposition) is the process of dividing a geometric figure into smaller (non-overlapping) recognizable shapes. |
The general purpose of decomposing is to have shapes within the given figure that can be more easily manipulated for computations. |
|
Let's take a look at some decomposing situations:
Given this figure, find its area, in square centimeters, using decomposition.
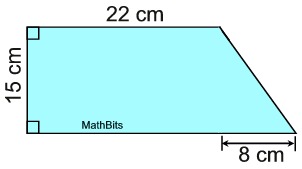
Note: Yes, this is a trapezoid. And yes, the area could be
found using the area formula for a trapezoid. But ... the question
asked for an answer using decomposition.
|
Solution: This figure is composed of a rectangle (notice the right angles) and a triangle. The diagram lends itself to being divided as shown.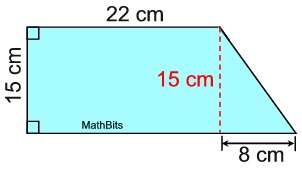 The area of the rectangle = 15 x 22 = 330.
The area of the rectangle = 15 x 22 = 330.
The area of right triangle = ½ (15) (8) = 60.
The area of the composite figure is
330 + 60
= 390 sq. cm. |

Given this figure, find its area, in square inches, using
decomposition.
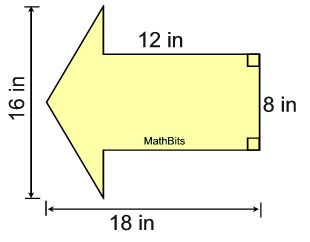
|
Solution: This figure is also composed of a rectangle (notice the right angles) and a triangle. The diagram can be divided as shown.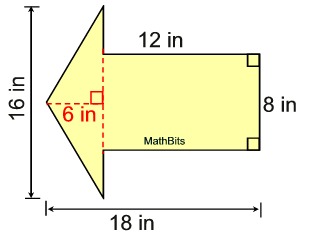 The area of the rectangle is 12 x 8 = 96.
The area of the rectangle is 12 x 8 = 96.
The area of the triangle is ½ (16)(6) = 48.
The area of the composite figure is
96 + 48 = 144 sq. in. |


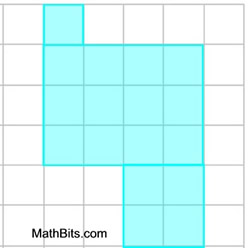
 In this example, the diagram is shown on a grid system to establish the lengths of the sides. This example also allows for simply "counting" to find the area, in addition to decomposing.
Given this figure, find its area,
in square grid units.
Solution: Finding the area of this shape is easy. We can just COUNT up the number of square grid units (single boxes) the shape is covering. It covers 17 square units, so the area is 17 square units. |
Let's take another look. Let's divide the figure into 3 rectangles (2 of which are squares).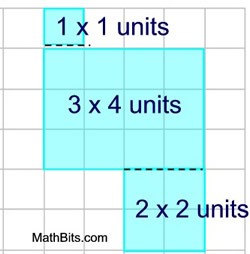
Solution: We can find the area of each rectangle
(A = bh) and then add up the three areas. This process DECOMPOSES the shape into figures whose areas are easily found.
Area = 1 + 12 + 4 = 17 square units.
|

Not all figures are presented on a grid, nor are the areas of all figures easily found on a grid.
As such, decomposing a figure into geometric shapes whose area can be easily determined, with a formula or method, is a valuable solution strategy.
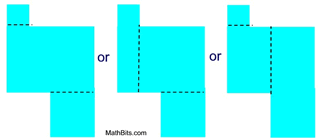
NOTE:
It may be possible to decompose a figure in a variety of patterns. As long as the areas of the newly formed shapes
can be easily determined (with formula or method), the choice of a decomposing pattern in not important. |
 |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|