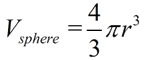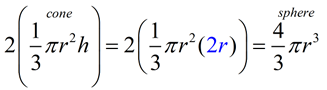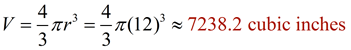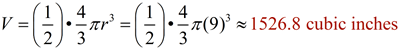|
 |
Spheres are three-dimensional closed surfaces.
They are not polyhedra since their faces
are curved surfaces, not polygons.
|
|
A sphere is a set of points in three-dimensional space equidistant from a point called the center. The surface of a sphere is perfectly round. |
Note: A "sphere" is the outer surface of a "ball" (or "solid sphere"). A "ball" is a sphere and everything inside the sphere.
The word "sphere" is from the Greek meaning "globe". |
|
Of all shapes, a sphere has the smallest surface area
for its volume. |
|
• |
Spheres are perfectly round geometric objects. |
• |
The intersection of a plane with a sphere is a circle (or a point if tangent to sphere). |
• |
If two planes are equidistant from the center of a sphere, and intersecting the sphere, the intersected circles are congruent.
|
|
• A great circle is the largest circle that can be drawn on a sphere. It will be drawn through a diameter of the sphere. Such a circle will be found when the cross-sectional plane passes through the center of the sphere.
•
The equator is an example of a great circle. Meridians (passing through the North and South poles) are also great circles.
• The shortest distance between two points on a sphere is along the arc of the great circle joining the points.
• The shortest distance between points on any surface is called a geodesic. In a plane, a straight line is a geodesic. On a sphere, a great circle is a geodesic.
| |
Let's check out distance on a sphere.
On a two-dimensional map of the Earth's surface, the shortest distance from California to Poland appears as a straight line. But when flying from California to Poland, flight plans usually fly over Iceland. The airplane is flying the shortest distance from California to Poland. Really?
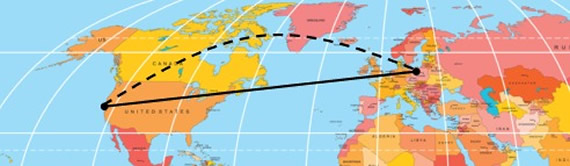
A map is a two-dimensional representation of a 3-dimensional surface of the Earth.
Remember that the Earth is modeled by a sphere.
As such, maps do not accurately represent Earth's dimensions
due to the distorted placement of the sections of the flat map.
A straight line on a map is not necessarily straight on a sphere.
Any circle passing through the center of the Earth will be a great circle.
The airplane is basically following a path along a great circle from California to Poland.
It is the shortest distance on Earth (a sphere), and the shortest distance from California to Poland.
If you can imagine gluing the map over a ball (a spherical shape), you will see that the "distances" are quite different on the sphere in comparison to what they appeared to be on the flat map. |
 |
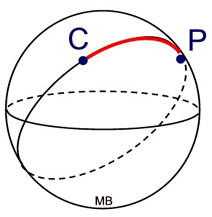
This great circle path on the sphere is called a geodesic.
A geodesic is the shortest distance between locations on a sphere.
Airplanes and ships travel in relation to great circles on the Earth's surface. |
 |
When flying in the airplane, it will appear (and feel) as if the plane is traveling in a straight line.
|
|

 Cross Sections
Cross Sections
are Circles
(or a tangent point) |
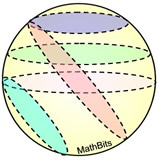
Cross Sections of a Sphere:
Unlike the cross sections of the other non-polyhedra shapes (cylinder and cone), a sphere has no base. So thinking of shapes parallel or perpendicular to the base of a sphere makes no sense.
All cross sections of a sphere are circles.
(All circles are similar to one another.) |

Volume of a Sphere:
Note: The volume of a sphere is actually the volume of the solid inside a sphere, often referred to as a spherical solid.
|
The volume inside of a sphere is four-thirds times π, times the cube of its radius. 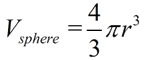 |
|
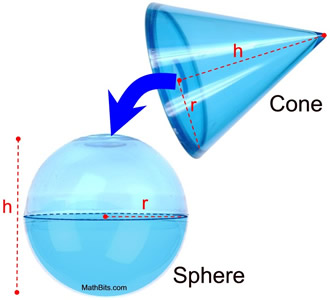
Justification of formula by "pouring" (sphere/cone):
We can conduct an experiment to demonstrate that the volume of a cone is half the volume of a sphere with the same radius and height. We will fill a right circular cone with water. When the water is poured into the sphere, it will take two cones to fill the sphere.
| • |
The radius of a right circular cone is r. |
| • |
The radius of a sphere is r. |
| • |
The height of the cone is h. |
| • |
The height of the sphere is h. |
| • |
In a sphere, height = 2 • radius. |
In Volume: 2(cones) = 1(sphere)
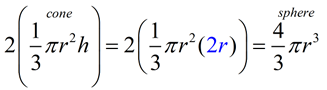 |
 |
Example:
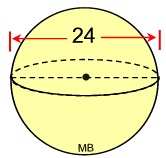
Find the volume of this sphere where the diameter is 24 units. Express answer to the nearest tenth of a cubic unit.
Solution:
• The diameter = 24, so the radius = 12 units.
• The volume formula is:
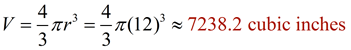 |
|
|

Surface Area of a Sphere:
|
The surface area of a sphere is four times the area of the largest cross-sectional circle, called the great circle.
SA = 4πr2 = πd2
SA = surface area; r = radius of sphere; d = diameter of sphere |
|
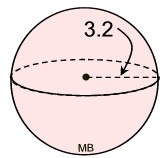
Example:
Find the surface of this sphere where the radius is 3.2 units. Express answer in terms of pi.
Solution:
• The radius = 3.2 units.
• The surface area formula is:
SA = 4πr2 = 4π(3.2)2 = 40.96π square units |
|
|

A hemisphere is the half sphere formed by a plane intersecting the center of a sphere. |
The cut-line forming a hemisphere is a great circle.
|
 |
The volume of a hemisphere is one-half the volume of a sphere.
However, when asked to find the surface area of a hemisphere,
be sure to read the question carefully.
|
Will the hemisphere's surface area
NOT include the base?
If so, the surface area is just half the
formula for the surface area of a sphere.
SA = 2πr2
|
Will the hemisphere's surface area
include the base?
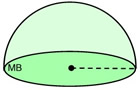
If so, add in the area of the circular base
which is the area of the great circle..
SA = 2πr2 + πr2
SA = 3πr2 |
If a question does not specify any information about the base, yet asks for the surface area,
you should assume that the base is to be included as part of the surface area.
Surface area, by definition, means the "covering of the entire surface",
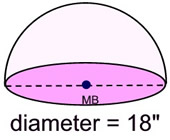
Example:
a) Find the volume of this hemisphere.
b) Find the surface area of this hemisphere with a closed base. Express answers to nearest tenths.
Solution:
a) The radius = 9 inches. The volume is ½ the volume of sphere formula:
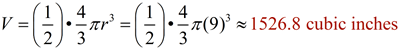
b) The surface area will be the formula:
 |
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|